Topic Menu

Cyber-chess a chess instruction site

Simple Harmonic Motion - Multiple Choice Questions

Q11. Which one of the following statements always applies to a damping force acting on a vibrating system?

A It is in the same direction as the acceleration.
B It is in the same direction as the displacement.
C It is in the opposite direction to the velocity.
D It is proportional to the displacement.

 

The damping force is a frictional force - it opposes motion - it is therefore ALWAYS in the opposite direction to velocity.

 

 

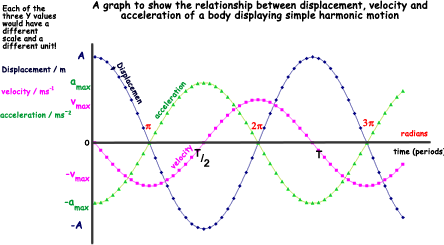
Q12. Which one of the following statements concerning the acceleration of an object moving with simple harmonic motion is correct?

A It is constant.
B It is at a maximum when the object moves through the centre of the oscillation.
C It is zero when the object moves through the centre of the oscillation.
D It is zero when the object is at the extremity of the oscillation.

 

Look at the graph - acceleration varies sinusoidally so choice A is incorrect.

At the centre of the oscillation x = 0

- when that is the case acceleration is also zero so choice B is untrue and C is true.

At the 'extremity' displacement is a maximum and acceleration is also maximum - but in the opposite direction - so D is untrue.

 

Q13. When the length of a simple pendulum is decreased by 600 mm, the period of oscillation is halved. What was the original length of the pendulum?

A
800 mm
B
1000 mm
C
1200 mm
D
1400 mm

Square the pendulum equation - as π and g are constant we get:

T2 = constant x L

We now have to do a bit of manipulation and simple algebra...

T12/L1 = T22/L2

L1= T12L2 /T22

L1 = L

L2 = L - 600

T1 = T

T2 = 0.5 T

L = T2(L - 600)/(0.5 T)2

L = 4(L - 600)

3L = 2400

L = 800 mm

(and therefore length of the second was 200 mm)

Double check

root 800 = 28.28

root 200 = 14.14 (half the value)

 

Q14. Which one of the following gives the phase difference between the particle velocity and the particle displacement in simple harmonic motion?

A
/4 rad
B
/2 rad
C
3/4 rad
D
2 rad

 

Look at the graphs - the peaks of displacement and velocity are 'out' from each other by a quarter of a cycle.

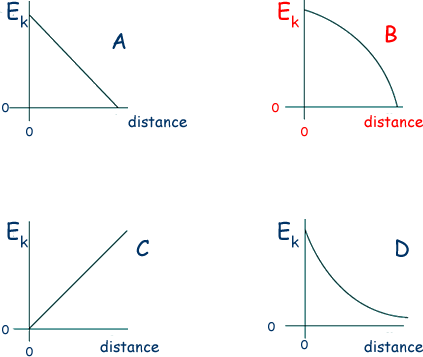
One cycle is 2 radians therefore they are 'out' by /2 radians.

 

 

Q15. A body executes simple harmonic motion. Which one of the graphs, A to D, best shows the relationship between the kinetic energy, Ek, of the body and its distance from the centre of oscillation?

 

KE relates to velocity squared.

When x = 0 velocity is a maximum - when x = A velocity = zero.

Therefore choice C is a non-starter.

KE = 1/2 mv2 = 22f 2(A2 - x2)

KE = a constant value - a constant multiplied by x2

An x2 graph curves upwards from the origin - you should know that from GCSE maths

The shape of the graph will therefore be that of choice B

 

 

Q16. The displacement (in mm) of the vibrating cone of a large loudspeaker can be represented by the equation x = 10 cos (150t), where t is the time in s. Which line, A to D, in the table gives the amplitude and frequency of the vibrations.
amplitude/mm
frequency/Hz
A
5
10/2
B
10
150
C
10
150/2
D
20
150/2

 

Look at the equation for displacement - A is the term before the 'cos'.

In this case '10' so the amplitude is 10

150 corresponds to 2f

so f = 150/2

Choice C

 

Q17. A mechanical system is oscillating at resonance with a constant amplitude. Which one of the following statements is not correct?

A The applied force prevents the amplitude from becoming too large.
B The frequency of the applied force is the same as the natural frequency of oscillation of the system.
C The total energy of the system is constant.
D The amplitude of oscillations depends on the amount of damping.

 

The applied force is what is producing resonance not limiting it - A is false.

Constant amplitude means that there is equilibrium - applied force's expected increase in the system's energy will be balanced by the system's loss of energy. C is true.

For resonance to occur B could be true - or the applied force could be at a multiple of the frequency - but for constant amplitude to be maintained the applied force would need to be at the frequency - no time for a slow down inbetween applications.

D is true - heavily damped systems have lower amplitude.

 

Q18. A particle of mass 0.20 kg moves with simple harmonic motion of amplitude 2.0 × 10–2m.

If the total energy of the particle is 4.0 × 10–5J, what is the time period of the motion?

A
π/4 seconds
B
π/2 seconds
C
π seconds
D
2π seconds

 

Total energy = max kinetic energy = 1/2 mv 2 at the centre of the path where velocity = maximum

vmax = ωA = 2πfA (from the circular motion equations!)

Total energy =1/2 m (2πfA)2 = 4.0 × 10–5

1/2 x 0.2 (2πf x2.0 × 10–2)2 = 4.0 × 10–5

4π2f2x 4.0 × 10–6 = 4.0 × 10–6

f2 = 1/(4π2)

T2 = 4π2

∴T = 2π - choice D

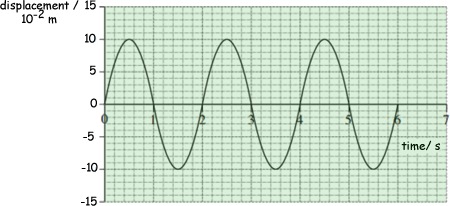
Q19. The graph shows the variation in displacement with time for an object moving with simple harmonic motion.

What is the maximum acceleration of the object?

A
0.025 m s–2
B
00.99 m s–2
C
002.5 m s–2
D
009.8 m s–2

 

Maximum acceleration = ω2A = (2πf)2A - from the data sheet

From the graph:

A = 10 x 10-2 m

T = 2 s

Now f = 1/T = 0.5 Hz

So, amax = (2π x 0.5)2 x 10 x 10-2

amax = π2 x 10 x 10-2 = 0.987m s–2 - choice B

 

Q20. Two pendulums, P and Q, are set up alongside each other. The period of P is 1.90 s and the period of Q is 1.95 s.

How many oscillations are made by pendulum Q between two consecutive instants when P and Q move in phase with each other?

A
19
B
38
C
39
D
78

 

The difference in time period is 0.05s - therefore to make up a complete extra swing P will move one more period than Q does in the same time.

Let number of swings of Q = n

Then n x 1.95 = (n+1) x 1.90

1.95n = 1.90n + 1.90

0.05n = 1.90

n = 38 - choice B