Nuclear Radius

Q6. The high energy electron diffraction apparatus represented in the diagram below can be used to determine nuclear radii. The intensity of the electron beam received by the detector is measured at various diffraction angles, θ.

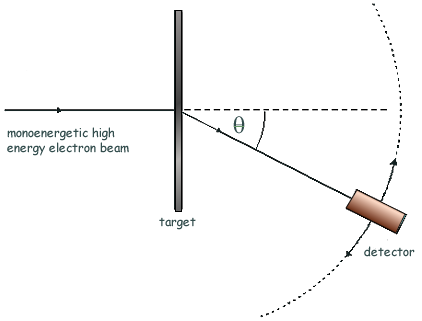
(a) Sketch on the axes below a graph of the results expected from such an electron diffraction experiment.

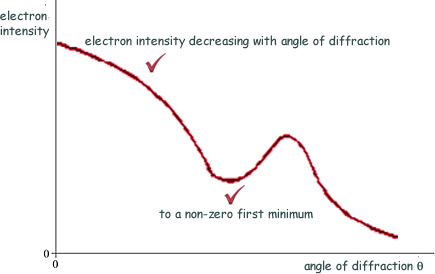
(2 marks)

(b)

(i) Use the data in the table below to plot a straight line graph that confirms the relationship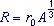

The obvious 'fill' for the last column is A^1/3allowing you to plot a graph with the gradient r₀

element	radius of nucleus R /10–15m	nucleon number; A	A1/3
lead	6.66	208	5.92
tin	5.49	120	4.93
iron	4.35	56	3.83
silicon	3.43	28	3.04
carbon	2.66	12	2.29

 

But you could decide to work out R³ and then plot R³ against A and have a gradient of r₀³

element	radius of nucleus R /10–15m	nucleon number; A	R3/10–45m3
lead	6.66	208	295
tin	5.49	120	165
iron	4.35	56	82.3
silicon	3.43	28	40.4
carbon	2.66	12	18.8

 

The value you are calculating should not be to more significant figures than the original value you cube.

It could be argues that the cube root of nucleon number could be to as many figures as you like as they are discrete values. But, you are using the table to plot a graph - more than 3sf would be pointless....

The first mark is for filling the last column correctly as above - all values! - quoting to the correct number of significant figures and fillimg in the heading correctly.

Two marks are for the plotting of the graph:

Choice of scale to make good use of the graph paper - axes covering more than 50% of graph sheet
Accuracy - all points plotted correctly using correctly labelled axes with units
(i.e. x-axis A^1/3, y-axis R/10^–15m or x axis A, y-axis R³/10^–45m³)

(ii) Estimate the value of r₀ from the graph.

r₀ has a unit - no unit no mark!

Stating that the gradient = r₀ [or gradient = r₀³]

Working out the value from your graph - r₀ = (1.1 ± 0.1) × 10^–15m

(5 marks)

(c) Discuss the merits of using high energy electrons to determine nuclear radii rather than using α particles.

Electrons are not subject to the strong nuclear force so electron scattering patterns are easier to interpret

Electrons give greater resolution

or electrons are more accurate because they can get closer

or α particles cannot get so close to the nucleus because of electrostatic repulsion

Electrons give less recoil.

(High energy) electrons are easier to produce than alpha particles

or electrons have a lower mass/ larger Q/m, so are easier to accelerate

In Rutherford scattering using α particles, the closest distance of approach, not R is measured

(3 marks maximum)

(Total 10 marks)