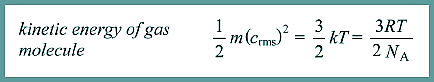Topic Menu

Cyber-chess a chess instruction site

Nuclear Radius

Q1. When a deuterium nucleus and a tritium nucleus overcome their Coulomb barrier and fuse together they may be considered as charged spheres in contact.

The constant ro which relates the nuclear radius, R, to the cube root of the mass number A may be assumed to be 1.3 fm.

(a)

(i) Calculate the radius of the deuterium nucleus RD and the radius of the tritium nucleus RT before fusion.

RD = 1.3 × 21/3 = 1.64 fm

RT = 1.3 × 31/3 = 1.87 fm

 

(ii) Calculate the minimum energy, in MeV, which must be supplied to the deuterium nucleus and the tritium nucleus when they fuse together.

The potential energy involved in putting two charges 'next' to each other is:

Ep = Q1Q2/(4πε0r)

This energy must be provided in order for fusion to occur:

r = (1.64 + 1.87) x 10-15 m

Both deuterium and tritium only have one proton so:

Q1 = Q2 =1.6 x 10-19 C

E= (1.6 x 10-19)2/(4πε0(3.51 x 10-15)

E = 6.56 × 10–14 J

E = 6.56 × 10–14/1.60 x 10-19 = 4.10 x 105 eV

E = 0.410 MeV

(5 marks)

(b) Estimate the temperature at which deuterium and tritium nuclei would have enough kinetic energy to undergo fusion.

To fuse they will have to be supplied with kinetic energy (from temperature rise) that equates with the potential energy required.

Energy of nucleus = 3/2 kT

6.56 × 10–14 = 3/2 × 1.38 × 10–23 × T

T = 3.2 × 109 K

This would be the temperature for the average atom to have energy to fuse, not all of them.

There would be a range of energies within the sample at this temperature - only half of them would have energy enough to fuse.

(3 marks)

(Total 8 marks)