Topic Menu

Cyber-chess a chess instruction site

Nuclear Fission

Q10. A space probe contains a small fission reactor, fuelled by plutonium, which is designed to produce an average of 300W of useful power for 100 years.

If the overall efficiency of the reactor is 10%, calculate the minimum mass of plutonium required.

energy released by the fission of one nucleus of

= 3.2 × 10–11 J

 

(Total 7 marks)

We first have to determine the time in seconds

100 years = 100 × 365.25 × 24 × 3600 seconds

100 y = 3.155 × 109 s

We know that we need power of 300 W - 300 J per second output

energy needed if 100% efficient = 3.155 × 109 × 300

It is only 10% effivient so the energy production has to be ten times greater

As it is only 10% efficient the energy needed = 3.155 × 109 × 300 × 10

= 9.465 × 1012 J

We are told how much energy comes from each fission so we can calculate the number of fissions needed

Number of fissions = 9.465 × 1012/3.2 × 10–11 = 2.96 × 1023

The minimum mass would be the mass of that number of plutonium atoms.

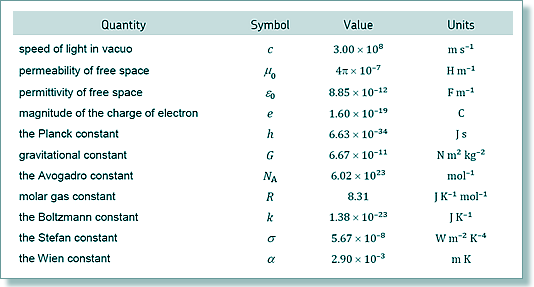
Number of moles = 2.96 × 1023/6.02 x 1023 = 0.492 moles

Now 1 mole has a mass of the nucleon number in grammes to the mass of 1 mol Plutonium is 239 g

so mass needed is 0.492 x 239 = 118 g

(Note that in this case you need to round up - as you are calculating minimum mass that would give that output. If you round down the mass would just short-change the energy required.)