Topic Menu

Cyber-chess a chess instruction site

E = mc2 - mass energy conversion

Q5.

(a) Calculate the binding energy, in MeV, of a nucleus of given that

the nuclear mass of = 58.93320 u

Binding energy = Mass of individual nucleons - Mass of nucleus

Mass defect Δm = Z mp + N mn – MCo

27 protons

59 - 27 = 32 neutrons

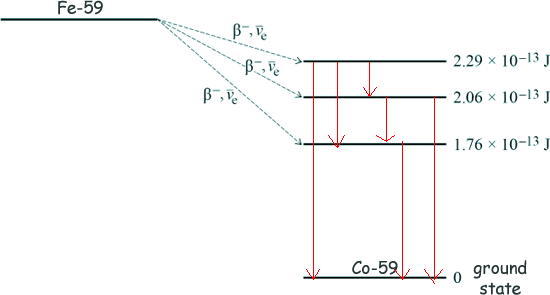
EBinding = (27 x 1.00728 + 32 x 1.00867) - 58.93320

EBinding = (27.19656 + 32.27744) - 58.93320

EBinding = 59.474 - 58.93320

EBinding = 0.5408u

Now, 1u = 931.5 MeV

∴  EBinding = 931.5 x 0.5408 MeV

EBinding = 503.8 MeV

[3 marks]

(b) A nucleus of iron decays into a stable nucleus of cobalt.

It decays by β− emission, followed by the emission of γ-radiation as the nucleus de-excites into its ground state.

The total energy released when the nucleus decays is 2.52 × 10−13 J.

The nucleus can decay to one of three excited states of the nucleus as shown in the diagram below - the energies of the excited states are shown relative to the ground state.

Calculate the maximum possible kinetic energy, in MeV, of the β− particle emitted when the nucleus decays into an excited state that has energy above the ground state.

Maximum kinetic energy will remain if the beta particle transfers to the 1.76 x 10-13 J state.

2.52 × 10−13 - 1.76 x 10-13 = 0.76 x 10-13J

Energy = 7.6 x 10-14J

1.6 x 10-13 J = 1 MeV

Energy = 7.6 x 10-14/(1.6 x 10-13 )

Energy = 0.48 MeV

[2 marks]

(c) Following the production of excited states of , γ-radiation of discrete wavelengths is emitted.

(i) State the maximum number of discrete wavelengths that could be emitted.

6 (see diagram)

[1 mark]

(ii) Calculate the longest wavelength of the emitted γ-radiation.

Longest wavlength is the lowest energy transfer:

ΔE = (2.29 - 2.06) x 10-13 J

ΔE = 0.23 x 10-13 J

E = hf = hc/λ

λ = hc/E

λ = 6.63 x 10-34x 3.0 x 10-8/(0.23 x 10-13)

λ = 8.65 x 10-12 m

[3 marks]

(Total 9 marks)