Topic Menu

Cyber-chess a chess instruction site

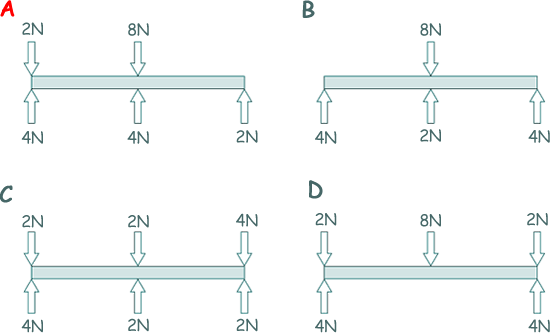
Moments

Q1. A light uniform rigid bar is pivoted at its centre.

Forces act on the bar at its ends and at the centre.

Which diagram shows the bar in equilibrium?

There are two things to consider here - moments and vertical up/down forces:

The bar is supported at the centre - therefore we can ignore all forces acting in the middle when calculating turning effects as they do not produce a moment.

A - clockwise forces 2N and 2N anticlockwise 4N (so in balance)

ΣUp forces = 10N

ΣDown forces = 10N (so in balance)

B - clockwise forces 4N anticlockwise 4N (so in balance)

ΣUp forces = 10N

ΣDown forces = 8N (so not in balance)

C - clockwise forces 8N anticlockwise 4N (so not in balance)

ΣUp forces = 6N

ΣDown forces = 8N (so in balance)

D - clockwise forces 6N anticlockwise 8N (so in balance)

ΣUp forces = 8N

ΣDown forces = 12N (so not in balance)

 

 

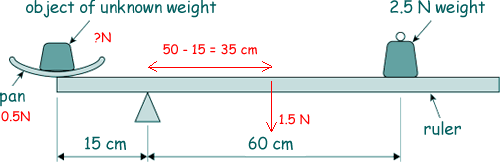
Q2. The diagram shows a uniform metre ruler of weight 1.5 N pivoted 15 cm from one end for use as a simple balance.

A scale pan of weight 0.5 N is placed at the end of the ruler and an object of unknown weight is placed in the pan.

The ruler moves to a steady horizontal position when a weight of 2.5 N is added at a distance of 60 cm from the pivot as shown.

What is the weight of the object?

A
9.5 N
B
10.0 N
C
13.0 N
D
13.5 N

Clockwise Moments

2.5 x 0.60 = 1.5 Nm

1.5 x 0.35 = 0.525 Nm

Anticlockwise Moments

0.15 x W = 0.15W Nm

By the Principle of Moments

ΣClockwise Moments = ΣAnticlockwise Moments

1.5 + 0.525 = 0.15W

2.025 = 0.15W

W = 2.025/0.15 = 13.5 N

But W = weight of the pan and the object - so the object weighs 13.5N - 0.5 N = 13.0 N

Choice C

This is a good example of how easy it is to get 'an answer' without taking all of the information into consideration.

I would always suggest getting into a habit of always marking all of the information from the written part of the question onto your diagram - that way you are less likely to forget something!