Topic Menu

Cyber-chess a chess instruction site

Moments

Q1.

(a) Define the moment of a force about a point.

For full marks just learn the definitions they give you on the syllabus!

A moment is the force multiplied by the perpendicular distance from the (pivot) point to the line of action of the force.

[2 marks]

(b) The diagram shows a gripper which is used for hand strengthening exercises.

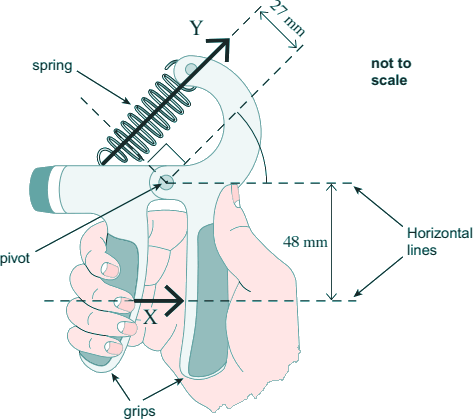
The diagram shows the gripper being squeezed.

In this situation, the gripper is in equilibrium.

The force produced by the fingers is equivalent to the single force X of magnitude 250 N acting in the direction shown in the diagram.

A force, Y, is exerted by the spring which obeys Hooke's law.

(i) Calculate the moment of force X about the pivot. State an appropriate unit.

Perpendicular distance from force X is 48 mm

d = 48 x 10-3m

F = 250 N

moment = Fd = 250 x 48 x 10-3 = 12 Nm

[2 marks]

(ii) Calculate force Y.

Perpendicular distance from force Y is 27 mm

d = 27 x 10-3m

F = ? N

There is equilibrium so the moment is 12 Nm

12 = F x 27 x 10-3

F = 12/(27 x 10-3) = 444 N

F = 440 N

[2 marks]

(iii) The extension of the spring is 15 mm. Calculate the spring constant k of the spring. Give your answer in N m–1.

F = kΔl

444 = k x 15 x 10-3

k = 444/(15 x 10-3)

k = 29600 N/m

k = 3.0 x 104 Nm-1

[2 marks]

(iv) Calculate the work done on the spring to squeeze it to the position shown in the diagram.

The work done on the spring is stored as energy:

E = 1/2 FΔl

E = 0.5 x 444 x 15 x 10-3

E = 3.3 J

[2 marks]

(Total 10 marks)