Topic Menu

Cyber-chess a chess instruction site

A level: Kinetic Theory Questions

Q10.

(a)

(i) Write down the equation of state for n moles of an ideal gas.

pV = nRT

(ii) The molecular kinetic theory leads to the derivation of the equation pV = 1/3 Nm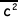 , where the symbols have their usual meaning.

State three assumptions that are made in this derivation.

Any three of the following:

all particles identical or have same mass

collisions of gas molecules are elastic

inter molecular forces are negligible (except during collisions)

volume of molecules is negligible (compared to volume of container)

time of collisions is negligible

motion of molecules is random

large number of molecules present (therefore statistical analysis applies)

monamatic gas (point particles)

Newtonian mechanics applies

(4 marks)

(b) Calculate the average kinetic energy of a gas molecule of an ideal gas at a temperature of 20 °C.

Temperature has to be in kelvin to use this equation so:

T = 273 + 20 = 293K

Ek = 3/2 kT

Ek = 1.5 x 1.38 × 10–23 x 293

Ek = 6.1 x 10-21 J

(3 marks)

(c) Two different gases at the same temperature have molecules with different mean square speeds. Explain why this is possible.

Ek is the same at a given temperature.

Kinetic energy is related to the mass and square of speed, therefore if the masses of the molecules are different the mean square speeds must be different, as the product of the mass and mean square speed must be kept constant.

(2 marks)

(Total 9 marks)