GCSE Questions - Forces
Q4. Beth wants to find out the depth of a well.
She thinks that she can calculate this by dropping a stone into the well and timing how long it takes to hear the stone splash at the bottom.
(a)
(i) Explain how she could use this measurement to find the depth of the well.
Explaining her known values: 
initial speed u = 0 m/s
acceleration due to gravity g (in these equations 'a') = 9.8 m/s
t = time from her stop watch
Using Newton's equation of motion:
s = ut + ½at2
we can directly calculate the distance s after putting in the values above
Or we could use:
v = u + at
to obtain the speed at which it hits the water.
and then use:
v2 - u2 = 2as to find s - the distance travelled.
[3 marks]
(ii) It takes 2.2 seconds for the stone to drop from rest and splash into the water at the bottom.
What is the speed of the stone when it hits the water?
v = u + at
v = 0 + 9.8 x 2.2
v = 21.56 m/s
v = 22 m/s
[2 marks]
(b) Describe the motion of the stone as it falls.
Assume it does not reach terminal velocity.
Use a free body diagram to help you.
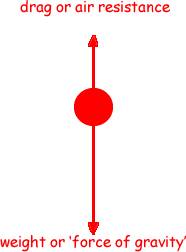
The free body diagram should only have two arrows drawn on it (or directions of the two forces should be described) – one upwards and one downwards
The arrows should be correctly named - weight and air resistance/drag
The downward arrow should be longer than upward arrow - forces should be unbalanced - there must be a resultant/net/overall force downwards so that object accelerates/gets faster/increases velocity or speed.
Two forces act on the stone - the force of gravity acting on its mass (its weight) pulls the stone vertically downward and makes it accelerate. As it picks up speed it interacts with a larger number of air particles, and these collisions form a drag force acting in opposition to its direction of travel (vertically upwards). This counter force gets larger as the speed of the stone increases - decreasing the acceleration it experiences as the net force acting on it is the difference between the two forces.
[4 marks]
(Total 9 marks)
About this site
You should always quote your final answer to the same number of sig figs as the values you are given.
