GCSE Questions: Energy Changes
Q9. The diagram shows a toy car in different positions on a racing track.
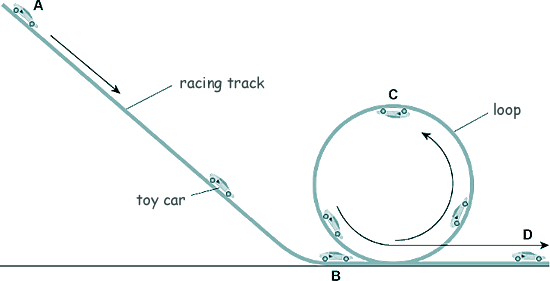
The toy car and racing track can be modelled as a closed system.
(i) Tick one of the statements below to explain why you think the toy car and racing track can be considered to be 'a closed system'.
| The racing track and the car both have gravitational potential energy. |
|
| The racing track and the car are always in contact with each other. |
|
| The total energy of the racing track and the car is constant. |
 |
[1 mark]
(ii) The car is released from rest at position A and accelerates due to gravity down the box track to position B.
mass of toy car = 0.040 kg
vertical height between position A and position B = 90 cm
gravitational field strength = 9.8 N/kg
Calculate the maximum possible speed of the toy car when it reaches position B.
At A:
EGPE = mgΔh
EGPE = 0.040 x 9.8 x 0.90
EGPE = 0.3528 J
EKE = ½mv2
EKE = 0J
Total energy = 0.3528 J
At B, if all of the gravitational potential energy it had at position A was transferred to kinetic energy then:
Total energy = 0.3528 J
EGPE = mgΔh
EGPE = 0
EKE = ½mv2
EKE = 0.3528 J
v2 = 0.3528 x 2/0.040
v2 = 17.64
v = 4.2 m/s
[5 marks]
(iii) At position C the car's gravitational potential energy is 0.20 J greater than at position B.
How much kinetic energy does the car need at position B to complete the loop of the track? Give a reason for your answer.
The KE needs to be more than 0.20 J because the car needs to be still moving at the top of the loop in order to complete the loop.
[2 marks]
[Total 8 marks]
About this site
Total energy = EGPE + EKE + energy transferred to the surroundings. 
