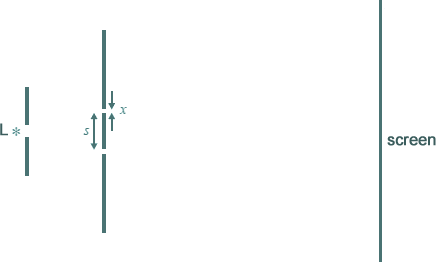Young's Slits Multiple Choice Solutions

Q1. In a double slit interference arrangement the fringe spacing is w when the wavelength of the radiation is λ, the distance between the double slits is s and the distance between the slits and the plane of the observed fringes is D.

In which one of the following cases would the fringe spacing also be w?

 

 

	wave length λ	distance between slits s	distance between slits and fringes D
A	2λ	2s	2D
B	2λ	4s	2D
C	2λ	2s	4D
D	4λ	4s	2D

 

For w to remain the same the product of λD must be the same as s - pencil in the values (I have in green!) you can then see that the answer is B as 2 x 2 = 4

Q2.

The diagram represents the experimental arrangement used to produce interference fringes in Young's double slit experiment.

The spacing of the fringes w on the screen will increase if:

A	the width of the single slit is increased - not in the equation!
B	the distance XY between the two slits is increased - bigger s
C	a light source of lower frequency is used - bigger λ
D	the distance between the single and double slits is decreased - smaller D

Write on the table what is happening to the elements in the equation... that makes it easy to see what happpens.

 

Q3.

Young's two slit interference pattern with red light of wavelength 7.0 × 10^–7 m gives a fringe separation of 2.0 mm.

What separation, in mm, would be observed at the same place using blue light of wavelength 4.5 × 10^–7 m?

A	0.65
B	1.3
C	2.6
D	3.1

 

fringe separation is the same as fringe spacing - w

w is proportional to λ

so x/2.0 = 4.5/7

x =9/7 = 1.3 = choice B

Q4.

Coherent monochromatic light of wavelength λ emerges from the slits X and Y to form dark fringes at P, Q, R and S in a double slit apparatus.

Which one of the following statements is true?

A       When the distance D is increased, the separation of the fringes increases. True! (But best to go through the others...)
B       When the distance between X and Y s is increased, the separation of the fringes increases.
C       When the width of the slit T is decreased, the separation of the fringes decreases. (is not in the equation)
D       There is a dark fringe at P because (YP − XP) is 2λ. (Whole numbers of wavelength path difference cause constructive interference - bright fringe)

Q5.

Interference fringes, produced by monochromatic light, are viewed on a screen placed a distance D from a double slit system with slit separation s. The distance between the centres of two adjacent fringes (the fringe separation) is w. If both s and D are doubled, what will be the new fringe separation?

A        ^w/₄

B       w

C       2w

D       4w

s and D being doubled cancels out - so w will be the same - choice B

 

Q6.

In a Young’s double slit interference experiment, monochromatic light placed behind a single slit illuminates two narrow slits and the interference pattern is observed on a screen placed some distance away from the slits.

Which one of the following decreases the separation of the fringes?

A       increasing the width of the single slit - Not in the equation
B       decreasing the separation of the double slits - decreasing s would make w bigger
C       increasing the distance between the double slits and the screen - increasing D would make w bigger
D       using monochromatic light of higher frequency - smaller λ.

Q7.

A double slit interference experiment is performed using monochromatic light of wavelength λ. The centre of the observed pattern is a bright fringe.

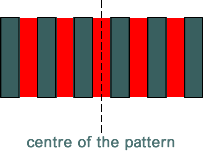
What is the path difference between two waves which interfere to give the third dark fringe from the centre?

A       0.5 λ
B       1.5 λ
C       2.5 λ
D       3.5 λ

Multiples of λ path difference causes bright fringes.

First dark fringe - 0.5 λ = second will be 1.5 λ and third 2.5 λ

Q8.

Interference maxima produced by a double source are observed at a distance of 1.0 m from the sources. In which one of the following cases are the maxima closest together?

A       red light of wavelength 700 nm from sources 4.0 mm apart
B       sound waves of wavelength 20 mm from sources 50 mm apart
C       blue light of wavelength 450 nm from sources 2.0 mm apart
D       surface water waves of wavelength 10 mm from sources 200 mm apart

Closest together maxima means w is smallest...

the slit distance (distance sources are apart) is of the same order for all of them mm

w is proportional to λ - the wavelengths of light are so small compared to sound and water .... so it must be A or C

for red the factor is 7/4 - for blue it is 4.5/2 = 9/4 - red makes is smallest - choice A

 

Q9.

In a double slit system used to produce interference fringes, the separation of the slits is s and the width of each slit is x.

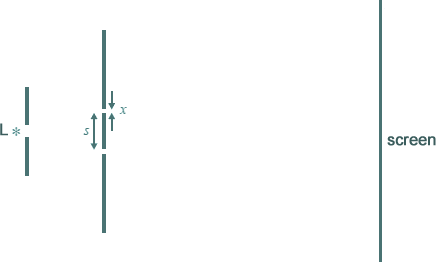
L is a source of monochromatic light.

Which one of the following changes would decrease the separation of the fringes seen on the screen?

A       moving the screen closer to the double slits - decreasing D - would make w smaller
B       decreasing the width, x, of each slit, but keeping s constant no effect 'x' is not in the equation
C       decreasing the separation, s, of the slits - would make w bigger
D       exchanging L for a monochromatic source of longer wavelength - would make w bigger

If ever the first choice is the answer always check them all.... under pressure in an exam you might make a mistake.... reason out all of them. You have about 2 minutes for a question....

Q10.

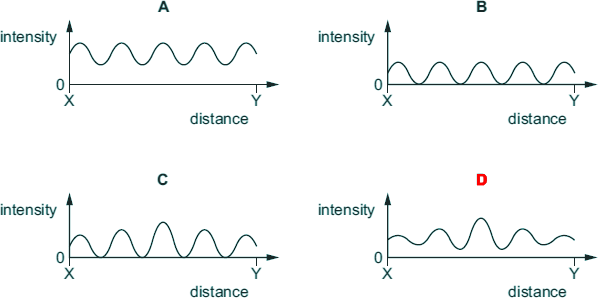
Two identical loudspeakers are connected in series to an a.c. supply, as shown.

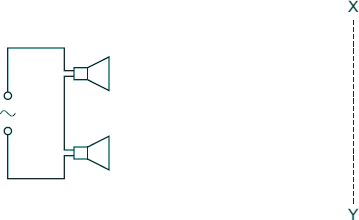
Which graph best shows the variation of the intensity of the sound with distance along the line XY?

This is a 'Young's Slits' for sound question.... You have two coherent sources that are difftacting and interferring to produce 'sound fringes'. Instead of variations in light intensity you would get variations in sound volume.

The sound will never be fully destructive so answers B and C are not true.

The sound will be loudest in the central position and gradually get of lower intensity. the 'fringe width' will be the same - Choice D