Solutions: Radioactivity Questions
Q8. The radioactive isotope of sodium 
has a half life of 2.6 years.
A particular sample of this isotope has an initial activity of 5.5 × 105 Bq (disintegrations per second).
(a) Explain what is meant by the random nature of radioactive decay.
.
There is equal probability of any nucleus decaying, it cannot be known which particular nucleus will decay next. 
The rate of decay is unaffected by the surrounding conditions,
It cannot be known at what time a particular nucleus will decay, it is only possible to estimate the proportion of nuclei decaying in the next time interval.
(2 marks MAX)
(b) On the axes below, sketch a graph of the activity of the sample of sodium over a period of 6 years.
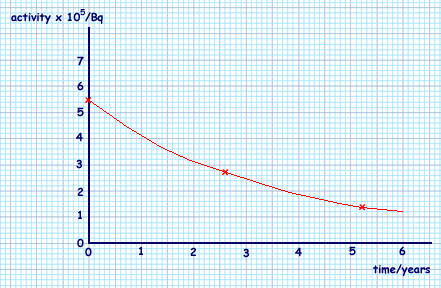
Marks awarded for a continuous curve starting at 5.5 × 105 Bq plus correct 1st half-life (2.6 yrs, 2.75 × 105 Bq correct 2nd half-life (5.2 years, 1.4 × 105 Bq)
(2 marks)
(c) Calculate
(i) the decay constant, in s–1, of ,
1 year = 3.15 × 107 s
= ln 2/(2.6 x 3.15 × 107) = 8.5 × 10–9 s–1
(ii) the number of atoms of in the sample initially,
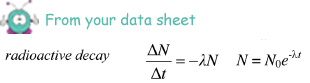
Initial decay rate = 
N0/t = 5.5 × 105 Bq
N =5.5 × 105/ 8.5 × 10–9
= 6.5 × 1013 (atoms)
(iii) the time taken, in s, for the activity of the sample to fall from 1.0 × 105 Bq to 0.75 × 105 Bq.
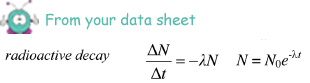
ln(0.75 × 105 /1.0 × 105 ) = - 8.5 × 10–9 x t
t = - (ln 0.75)/8.5 × 10–9
= 3.4 × 107 s
(6 marks)
(Total 10 marks)
About this site
