Topic Menu

Cyber-chess a chess instruction site
Solutions: Radioactivity Questions

Q6. A radioactive nuclide decays by emitting particles. The graph shows how the rate of decay At of the source changes with time t

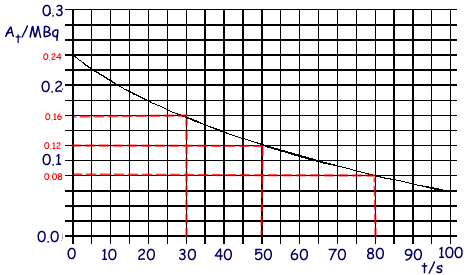
(a) Determine

(i) the half-life of the nuclide,

From the graph - 50 seconds

(ii) the decay constant,

= ln 2 / 50 = 0.0139

= 0.014 s-1(unit required!)

(iii) the initial number of undecayed nuclei present at time t = 0.

At = 0.24 MBq at time t = 0s

N = A/

= 0.24 x 106/0.0139

= 1.71 x 107

= 1.7 x 107

(5 marks)

(b) Each decay releases 1.0 x 10–12J.

For the time interval between t = 30s and t = 80s, calculate:

(i) the number of nuclei which decay,

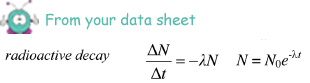
At 30 seconds

N = 1.71 x 107 x e (-0.014 x 30)

N = 1.12 x 107

At 80 seconds

N = 1.71 x 107 x e (-0.014 x 80)

N = 0.56 x 107

during the time interval

1.12 x 107- 0.56 x 107 = 0.56 x 107

(ii) the energy released.

Total energy released = 0.56 x 107 x 1.0 x 10–12J

= 5.6 mJ

(4 marks)

(Total 9 marks)