Solutions: Radioactivity Questions
Q2.
(a)
(i) What is meant by the random nature of radioactive decay?
Which atom decays at what time is pure chance
at what time is pure chance
(ii) Explain what is meant by each of the following:
( 6 marks)
(b) The radioactive isotope of iodine 131I has a half-life of 8.04 days. Calculate
(i) the decay constant of 131I,

(8.04 x 24 x 602) = ln 2/
 = ln 2/ (8.04 x 24 x 602)
= ln 2/ (8.04 x 24 x 602)  = 1.0 x 10-6 s-1
= 1.0 x 10-6 s-1 
(ii) the number of atoms of 131I necessary to produce a sample with an activity of 5.0 × 104 disintegrations s–1 (Bq),
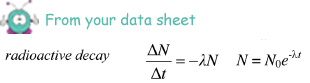
5.0 × 104 = - x N
x N
N = - 5.0 × 104/ 
N = - 5.0 × 104/(answer to part (i))
N = - 5.0 × 104/1.0 x 10-6
N = 5.0 x 1010
(iii) the time taken, in hours, for the activity of the same sample of 131I to fall from 5.4 × 104 disintegrations s–1 to 5.0 × 104 disintegrations s–1
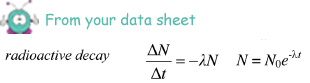




ln (5.0 × 104/ 5.4 × 104) = -  t
t 
- 0.077 = -1.0 x 10-6t
t = 0.077/1.0 x 10-6 = 7.7 x 104s
7.7 x 104/602 = 21 hours 
(6 marks)
(Total 12 marks)


