Q12. The isotope of uranium, , decays into a stable isotope of lead, by means of a series of α and β– decays.

(a) In this series of decays, α decay occurs 8 times and β– decay occurs n times. Calculate n.

8 alphas will reduce the nucleon number by 8 x 4 = 32 and the proton number by 8 x 2 = 16

For beta decay proton number increases by one and the nucleon number stays the same. We must therefore look at the proton number to find out how many betas occur.

92 - 16 = 76 and

The final proton number is 82 - there are therefore 82 - 76

= 6 beta decays.

(1 mark)

 

(b)

(i) Explain what is meant by the binding energy of a nucleus.

The binding energy of a nucleus is the energy required to split the nucleus up into its individual neutrons and protons (or nucleons)nucleons

OR the energy released to form the nuleus from its individual neutrons and protons/nucleons

(2 marks)

(ii) The graph belowshows the binding energy per nucleon for some stable nuclides.

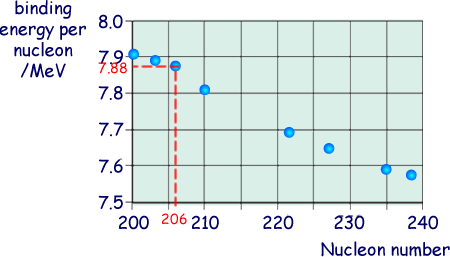
Estimate the binding energy, in MeV, of the nucleus.

From the graph the binding energy per nucleon is 7.88 MeV

We have 206 nucleons, so the total binding energy is 206 x 7.88 = 1620 MeV

(Any answer between 1600 and 1640 MeV was accepted)

(1 mark)

(c) The half-life of is 4.5 × 10⁹ years, which is much larger than all the other half-lives of the decays in the series. A rock sample when formed originally contained 3.0 × 10²² atoms of and no atoms.

At any given time most of the atoms are either or with a negligible number of atoms in other forms in the decay series.

(i) Using the axes below, sketch graphs to show how the number of atoms and the number of atoms in the rock sample vary over a period of 1.0 × 10¹⁰ years from its formation.

Label your graphs U and Pb.

After one half life the number of uranium atoms will have halved - after a further half life time period that value will have halved.

Put a cross at each of these positions and draw in a smooth curve that indicated exponential decay.

The lead count increases as the uranium decreases - the sum of the lead and uranium will be constant. Lead starts at zero and at the first half life will equal that of uranium - as half of the atoms have changed... by the time only a quarter of the atoms are uranium three quarters will be lead.

The examiner gives marks for your line actually passing through the correct points.

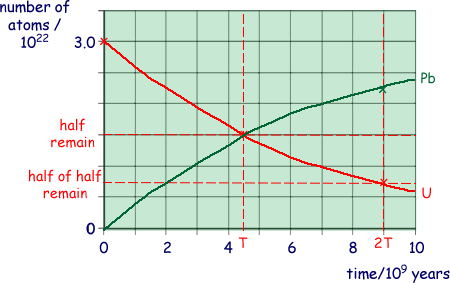
U, a graph starting at 3.0 × 10²² showing exponential fall passing through 0.75 × 10²² at 9 × 10⁹ years

Pb, inverted graph of the above so that the graphs cross at 1.5 × 10²² at 4.5 × 10⁹ years

(2 marks)

(ii) A certain time, t, after its formation the sample contained twice as many atoms as atoms.

Show that the number of atoms in the rock sample at time t was 2.0 × 10²².

Let number of uranium atoms be U and number of lead atoms be Pb

At time t

U + Pb = 3.0 × 10²²

But U = 2Pb

So, U + 0.5U = 3.0 × 10²²

U = 3.0 × 10²²/1.5 = 2.0 × 10²²

(1 mark)

(iii) Calculate t in years.

N = N_o e^-λt

2 × 10²² = 3 × 10²² × e^-λt 

ln (2/3) = -λt

ln (3/2) = ln 1.5 = λt

t = ln 1.5 / λ

Now λ = ln 2 / t_1/2

λ = ln 2 / 4.5 × 10⁹

λ = 1.54 × 10^-10

t = ln 1.5/ 1.54 × 10^-10

t = 2.6 × 10⁹ years

The answer of 2.7 × 10⁹ years was also accepted - it depends on how you round...

(3 marks)

(Total 10 marks)