Topic Menu

Cyber-chess a chess instruction site
Solutions: Radioactivity Questions

Q1.

(a)

(i) Sketch a graph to show how the neutron number, N, varies with the proton number, Z, for naturally occurring stable nuclei over the range Z = 0 to Z = 90. Show values of N and Z on the axes of your graph and draw the N = Z line.

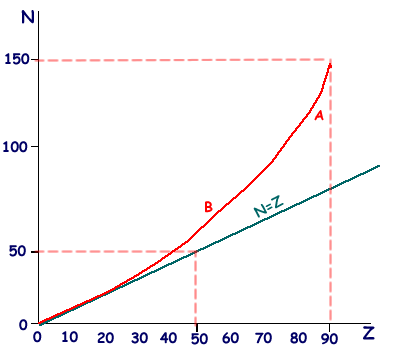
(ii) On your graph mark points, one for each, to indicate the position of an unstable nuclide which would be likely to be an emitter, labelling it A, a emitter, labelling it B.

N=Z line should have dashed guides from the axes to show it is correct.

Scales on graph

- should go to 90 on the x-axis (you are asked to do this as naturally occurring isotopes only go up to uranium (92))

- the neutron number corresponding to 90 should be about 150

Stability line should follow the N=Z line up to Z=20. It should then curve upwards towards a point where N = 150 and Z = 90.

Alpha emitters need to lose mass (you don't get them for Z<60) and positive charge. They are therefore high up and below the stability line. See graph for A

Beta emitters have too many neutrons - they are therefore above the stability line. See graph for B

(5 marks)

(b) State the changes in N and Z which are produced in the emission of

(i) an particle,

N decreases by 2; Z decreases by 2

(ii) a particle.

N decreases by 1; Z increases by 1

(2 marks)

(c) The results of electron scattering experiments using different target elements show that

where A is the nucleon number and ro is a constant. Use this equation to show that the density of a nucleus is independent of its mass.

Denisty = mass/molume = m/V

Now, mass (m) is proportional to A (number of nucleons in the nucleus)

and volume (V) is proportional to R3, from the equation above we see that R is proportional to the cube root of A; therefore Volume V is proportional to A

Therefore density is proportional to A/A = 1. (The dependency on A of both mass and volume cancels out when you combine them as density).

i.e. density is independent of A.

(3 marks)

(Total 10 marks)