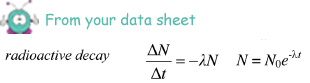Q1. A student attempted to determine the half-life of a radioactive substance, which emits particles, by placing it near a suitable counter. He recorded C, the number of counts in 30 s, at various times, t, after the start of the experiment. The results given in the table were obtained.

(a) Explain what is meant by half-life. (1 mark)

The half life of a radioactive isotope is the time taken for half of the radioactive nuclei (of that isotope) to decay.

(b) Complete the table. (1 mark)

Correct values of ln C The values should be quoted to 3sf (one more than the data - and ideal for plotting a graph)

(c) On the graph paper

(i) plot ln C against t,

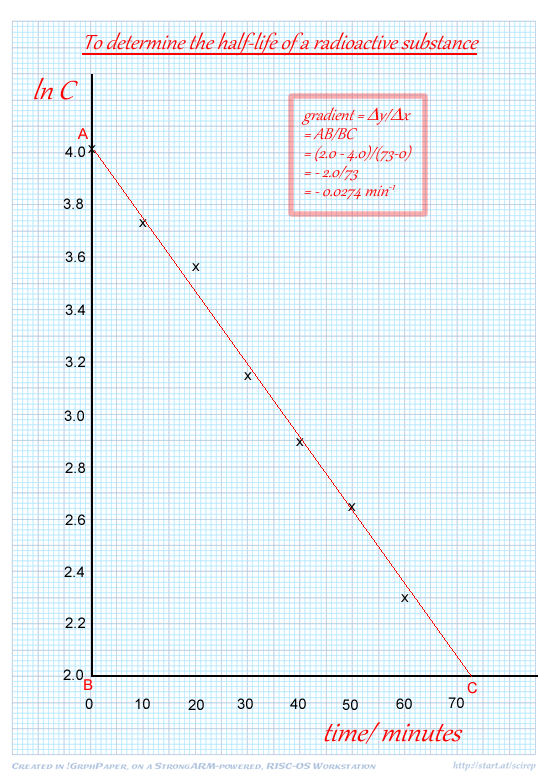
seven points correctly plotted (lose one mark for each incorrect point)

axes labelled with units - scale making graph fill more than half of the paper in both x and y directions

(ii) draw the best straight line through your points,

Line with equal number of points either side

(iii) determine the gradient of your graph.

See the graph above:

Clearly using a large triangle on graph

Always use a large triangle

Label the vertices ABC and relate the triange to dy/dx and gradient

gradient =– (value that rounds to 0.03) min ^–1

Note that omitting the sign and unit for the gradient loses you two possible marks!

(5 MAX marks)

(d)

(i) Show that the decay constant of the substance is equal to the magnitude of the gradient of your graph.

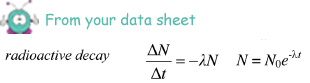
so,

The activity is related to the 'count' - as the number registered on the counter is proportional to the activity of the sample.

so,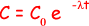

Therefore:

ln C – ln C₀ = – t

Relating this to the equation for a straight line: y = mx + c,

we get

ln C = – t + ln C₀

where

lnC relates to y

t relates to x

– relates to m (gradient)

and ln C₀ relates to c (intercept)

Therefore plotting a graph of 'lnC' against 't' gives you a negative gradient of (the decay constant)

(ii) Calculate the half-life of the substance.

Half life = ln 2/(value for that you calcuated from your graph)

ln2/0.0274 = 25 minutes mark for unit not absolute value

(3 marks MAX)

(e) This particular experiment is likely to lead to an inaccurate value for the half-life. Suggest two ways in which the accuracy of the experiment could be improved.

• Count over longer period than half minute [or repeat experiment]
• Use stronger source or place the source closer to the GM tube.
• Determine a background count and correct the count obtained by deducting that value to give a 'corrected count'.

(2 marks MAX)

(f) The age of a piece of bone recovered from an archaeological site may be estimated by ¹⁴C dating. All living organisms absorb ¹⁴C but there is no further intake after death. The proportion of ¹⁴C is constant in living organisms.

• A 1 g sample of bone from an archaeological site has an average rate of decay of 5.2 Bq due to ¹⁴C.
• A 1 g sample of bone from a modern skeleton has a rate of decay of 6.5 Bq.

(The counts are corrected for background radiation).

Calculate the age, in years, of the archaeological samples of bone.

Half life of ¹⁴C = 5730 years

For carbon 14

= ln 2/5730 = 1.210 x 10^-4 year^-1

 

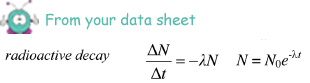
ln (5.2/6.5) = -1.21 x 10^-4x t

t = - ln (5.2/6.5)/(1.21 x 10^-4 ) = 0.184 x 10⁴

= 1840 years

(4 marks)

(Total 16 marks)