Solutions: Medical Option - the EYE
Q1.
A convex lens is placed 0.25 m from an object.
The focused image produced is virtual and is 0.60 m from the lens.
(a) Calculate
(i) the power of the lens,
v = -0.60 m
u = 0.25 m
f = ?
P = 1/f = 1/u + 1/v = 1/0.25 - 1/0.60 = 2.33  D
D 
(ii) the magnification produced.
M = v/u = 0.6/0.25 = 2.4
(3 marks)
(b) Draw a ray diagram to show the formation of the image produced by this lens. The diagram does not have to be to scale, but relevant distances must be marked.
diagram to show:
- two correct rays to locate image - through pole of lens and parallel to the principal axis and then through focal point

- correct (virtual, upright) image

- two distances (u and v) shown

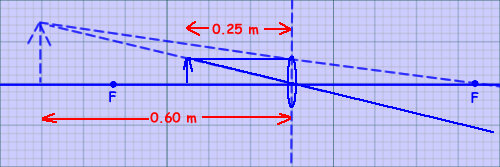
(3 marks)
(c)
(i) What defect of vision is this lens used to correct?
Longsightedness - hypermetropia
(ii) A person has an unaided near point at 0.60 m and an unaided far point at infinity. Calculate the range of vision of the person when using this lens.
v = -0.60 m
u = ?
1/f = 2.33 D
1/f = 1/u + 1/v
1/u = 1/f - 1/v = 2.33 + 1/0.60 = 4.0 u = 0.25 m
The person's range of vision will therefore be from 0.25m  to 0.43 m
to 0.43 m 
(4 marks)
(Total 10 marks)


