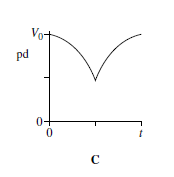Capacitors - Multiple Choice Solutions

Q1. A 1μF capacitor is charged using a constant current of 10 μA for 20 s. What is the energy finally stored by the capacitor?

E = ½ Q V = ½ C V² = ½ Q²/ C

Q = It

E = ½ (It)²/C

E = ½ (10 x 10^-6 x 20)²/10^-6

E = 0.02 J (Choice B)

A      2 × 10^-3 J
B      2 × 10^-2 J
C      4 × 10^-2 J
D      4 × 10^-1 J

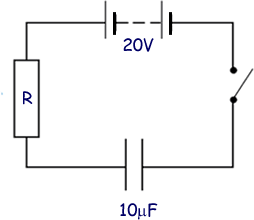
Q2. A capacitor of capacitance 10 μF is fully charged through a resistor R to a p.d. of 20V using the circuit shown below.

Which one of the following statements is incorrect?

A The p.d. across the capacitor is 20V. True

B The p.d. across the resistor is 0V. True

C The energy stored by the capacitor is 2mJ.

E = ½ Q V = ½ C V² = ½ Q²/ C

= ½ 10 x 10^-6 x 20²

= 5 x 10^-6 x 400

= 2 x 10^-3 J - so C is true

D The total energy taken from the battery during the charging process is 2 mJ.

The energy stored is 2 mJ – but energy will be dissipated as current passes through the resistor and battery – so total energy taken to store that charge will be greater than that.

Q3. A 10 mF capacitor is charged to 10V and then discharged completely through a small motor. During this process, the motor lifts a weight of mass 0.10 kg. If 10 % of the energy stored in the capacitor is used to lift the weight, through what approximate height will the weight be lifted?

The energy stored in the capacitor is used to power the motor… well 10% of it anyway!

So, as E = ½ Q V = ½ C V² = ½ Q²/ C

10% of E = 0.10 x ½ 10 x 10^-3 x 10² = 0.05 J

work done = mg=Δh

0.05 = 0.10 x 9.81 x Δh

Δh = 0.05m

A 0.05 m

B 0.10 m

C 0.50 m

D 1.00 m

 

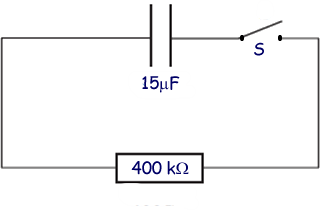
Q4. A capacitor of capacitance 15 μF is fully charged and the potential difference across its plates is 8.0V. It is then connected into the circuit as shown below.

The switch S is closed at time t = 0. Which one of the following statements is correct?

A The time constant of the circuit is 6.0 ms.

time constant = RC = 400 x 10³ x 15 x 10^-6 = 6.0s - so this wrong!

B The initial charge on the capacitor is 12 μC.

It will be 15 μF when fully charged - it will hold its full capacity - so this is wrong!

C After a time equal to twice the time constant, the charge remaining on the capacitor is Q₀e², where Q₀ is the charge at time t = 0.

Q = Q₀e^-t/RC

if t = 2 x RC then t/RC will be 2

We will therefore get Q₀e^-2 not Q₀e² - so this is wrong!

D After a time equal to the time constant, the potential difference across the capacitor is 2.9V

This ought to be correct - but we have to check!

V = V₀e^-t/RC

V = 8e^-1

V = 2.94 True

Q5. A capacitor of capacitance C discharges through a resistor of resistance R. Which one of the following statements is not true?

A The time constant will increase if R is increased.

time constant = RC – so this is true

B The time constant will decrease if C increased.

time constant = RC – so this is false

C After charging to the same voltage, the initial discharge current will increase if R is decreased.

If you reduce the resistance current increases so this is true.

D After charging to the same voltage, the initial discharge current will be unaffected if C is increased.

Current and voltage are linked by the resistance not the capacitance – so this is true.

 

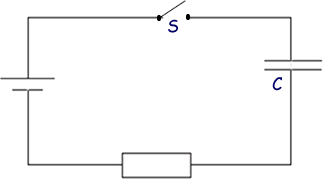
Q6. In the circuit shown below, the capacitor C is charged to a potential difference V when the switch S is closed.

Which line, A to D, in the table gives a correct pair of graphs showing how the charge and current change with time after S is closed?

• The charge will start at zeo - there is no charge on the plates until you close the switch. Therefore graph 2 must show you what charge is doing.
• When the switch is closed the charge build up will be rapid at first, but later charge build up will be slower because of repulsion from same charge particles.
• The rate at which charge is transferred is the current. Therefore the current graph is graph 1 - large current reducing exponentially to zero as the plates charge up to capacity.

	CHARGE	CURRENT
A	graph 1	graph 1
B	graph 1	graph 2
C	graph 2	graph 1
D	graph 2	graph 2

 

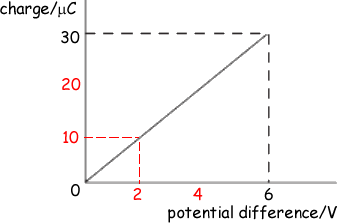
Q7. The graph shows how the charge stored by a capacitor varies with the potential difference across it as it is charged from a 6V battery.

Which one of the following statements is not correct?

A The capacitance of the capacitor is 5.0 μF.

C = Q/V = 30μ/6 = 5 μF

B When the potential difference is 2V the charge stored is 10 μC.

See graph - correct

C When the potential difference is 2V the energy stored is 10 μJ.

Area under graph (equiv to ½ QV) = energy = ½(2 x 10) = 10 μJ = correct

D When the potential difference is 6V the energy stored is 180 μJ.

Area under graph (equiv to ½ QV) = energy = ½(30 x 6) = 90 μJ - incorrect

Q8. A capacitor of capacitance C stores an amount of energy E when the pd across it is V. Which line, A to D, gives the correct stored energy and pd when the charge is increased by 50% ?

 

 

E = ½ QV = ½ CV² = ½ Q²/C

A one

B two

C three

D four

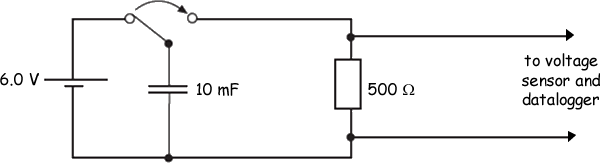
Q10. A voltage sensor and a datalogger are used to record the discharge of a 10 mF capacitor in series with a 500Ω resistor from an initial pd of 6.0V. The datalogger is capable of recording 1000 readings in 10s.

Which line, A to D, in the table gives the pd and the number of readings made after a time equal to the time constant of the discharge circuit?

Time constant = CR = 10 x 10^-3 x 500 = 5s

Datalogger gives 100 readings per second

Therefore in 5s it will give 500 readings.

-----------------------

V = V₀e^-t/RC

V = V₀e^-1

V = 6.0 x 0.368 = 2.2 volts

 

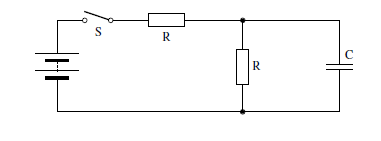
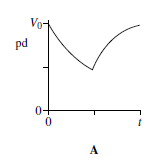
Q11. When switch S in the circuit is closed, the capacitor C is charged by the battery to a pd V₀.
The switch is then opened until the capacitor pd decreases to 0.5 V₀, at which time S is closed
again. The capacitor then charges back to V₀.

Which graph best shows how the pd across the capacitor varies with time, t, after S is opened?

 

Choice A - the capacitor is fully charged at time t=0... it then discharges. Discharge is exponential... therefore A or B fit the bill. On recharge, pd will increase exponentially (most rapidly at first), therefore it must be A.

Q12. A 2.0 mF capacitor, used as the backup for a memory unit, has a potential difference of 5.0V across it when fully charged. The capacitor is required to supply a constant current of 1.0μA and can be used until the potential difference across it falls by 10%.

How long can the capacitor be used for before it must be recharged?

A	10 s
B	100 s
C	200 s
D	1000 s

V = IR

R = V/I = 5.0/(1.0 x 10^-6) = 5 x 10⁶ Ω

---------------------

time constant = RC = 5 x 10⁶ x 2.0 x 10^-3 

RC = 1.0 x 10⁴ s

----------------------

V = V₀e^-t/RC

If the voltage falls by 10% it will then be 0.9V₀

0.9 = e^-t/10000

t = -ln 0.9 x 10000 = 1059s

Therefore the answer is choice D

Q13. When a capacitor discharges through a resistor it loses 50% of its charge in 10 s. What is the time constant of the capacitor-resistor circuit?

 

Q = Q₀e^-t/RC

If the charge falls by 50% it will then be 0.5 Q₀

0.5 = e^-10/RC

ln 0.5 = -10/RC

RC = -10/ln 0.5

RC = 14s (Choice C)

Q14. An uncharged capacitor of fixed capacitance is connected in series with a switch and battery. The switch is closed at time t = 0.

Which graph, A to D, shows how the energy, E, stored by the capacitor, changes with time, t, after the switch is closed?

Energy stored = ½ QV = ½ CV² = ½ Q²/C

The voltage across the capacitor will be the same as graph A - the energy stored will therefore be that graphline value squared - which will be a similar shape - choice A

Choice D is not possible as energy stored will increase and be zero at time zero.

Choice C is a steady increase with time and we know that voltage increase is rapid at first.

Choice B is not possible because the voltage increase and therefore the energy stored will level off towards completion of the charge.

 

Q15.The voltage across a capacitor falls from 10 V to 5 V in 48 ms as it discharges through a resistor. What is the time constant of the circuit?

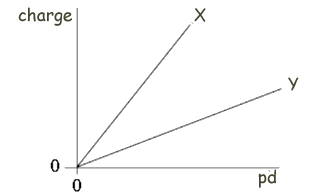
V = V₀e^-t/RC

5 = 10 e^{-0. 48/RC}

ln 0.5 = -0.048/RC

RC = - 0.048 /ln 0.5

RC = 0.069s = 69ms

Q16. The graph shows how the charge stored by each of two capacitors, X and Y, increases as the pd across them increases. Which one of the following statements is correct?

Q = CV

Therefore as V increases Q will increase

C is constant - the gradient of the graph.

X has a bigger gradient so the capacitance of X is greater than the capacitance of Y.

Q17. A 1000 μF capacitor and a 10 μF capacitor are charged so that the potential difference across each of them is the same. The charge stored in the 1000 μF capacitor is Q₁ and the charge stored in the 10 μF capacitor is Q₂.

What is the ratio Q₁/Q₂?

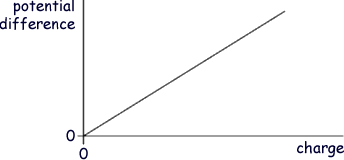
Q = CV

V = Q/C

Therefore Q₁/C₁ = Q₂/C₂

Q₁/Q₂= C₁ /C₂ = 1000/10 = 100 - Choice A

Or you can just reason it - capacitor 1 has 100 times the capacitance of capacitor 2 - therefore it will store 100 times more charge as it has a 100x capacity for charge!

Q18. The graph shows how the potential difference across a capacitor varies with the charge stored by it.

Which one of the following statements is correct?

Q = CV

therefore V = Q/C

V = ¹/_C x Q

this corresponds to y = mx

The gradient is therefore ¹/_C

Energy stored is the area under the graph line not the gradient.

A The gradient of the line equals the capacitance of the capacitor. Wrong!

B The gradient of the line equals the energy stored by the capacitor. Wrong!

C The reciprocal of the gradient equals the energy stored by the capacitor. Wrong!

D The reciprocal of the gradient equals the capacitance of the capacitor. True!

Q19. An initially uncharged capacitor of capacitance 10 μF is charged by a constant current of 200 μA. After what time will the potential difference across the capacitor be 2000V?

Q = CV

Q = 10 x 10^-6 x 2000 = 0.020 coulombs

I = Q/t

t = Q/I = 0.020/(200 x 10^-6) = 100 s

A 50 s

B 100 s

C 200 s

D 400 s

Q20. A 1000 μF capacitor, X, and a 100 μF capacitor, Y, are charged to the same potential difference.

Which row, A to D, in the table gives correct ratios of charge stored and energy stored by the capacitors?

Charge stored = CV = 1000μ/100μ = 10

-------------------------

Energy stored = ½ QV = ½ CV² = ½ Q²/C

V is constant so energy stored depends on C

ratio will be 1000μ/100μ = 10