Capacitor Questions
Q7. A student was required to design an experiment to measure the acceleration of a heavy cylinder as it rolled down an inclined slope of constant gradient. He suggested an arrangement that would make use of a capacitor-resistor discharge circuit to measure the time taken for the cylinder to travel between two points on the slope.
The principle of this arrangement is shown in the diagram below.
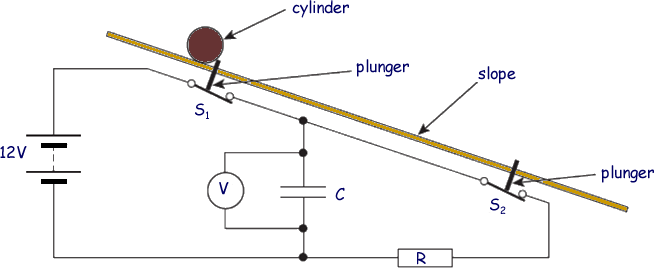
S1 and S2 are two switches that would be opened in turn by plungers as the cylinder passed over them. Once opened, the switches would remain open. The cylinder would be released from rest as it opened S1. The pd across the capacitor would be measured by the voltmeter.
(a) Describe the procedure the student should follow, including the measurements he should make, when using this arrangement. Explain how he should use the measurements taken to calculate the acceleration of the cylinder down the slope.
Measurements
● initial pd across C (V0) from voltmeter (before releasing roller)
● distance 's' along slope between plungers using a metre rule or tape
● final pd across C (V1) from voltmeter
● measurements repeated to provide a more reliable result
Analysis
● time t is found from V1 = V0e-t/RC, giving t = RC ln (V0/V1)
● Using Newton's equations of motion s = ut + ½ at2 where u = 0, therefore acceleration a = 2s/t2
● repeat and find average 'a' from several results OR finding t for several different values of s you could plot a graph of t2 against s. the gradient of the graph would be equal to 2/a
(6 marks)
(b) When the student set up his experiment using the arrangement shown above, he used a 22 μF capacitor, C, and a 200 kΩ resistor, R. In one of his results, the initial pd was 12.0 V and the final pd was 5.8V. The distance between the plungers was 2.5 m.
(i) From the student's result, calculate the time taken for the cylinder to reach the second plunger.
RC = 22 × 106 × 200 × 103
RC = 4.40 = 4.4 s 
V1 = V0e-t/RC
t = RC ln (V0/V1)
t = 4.40 ln (12.0/5.8) 
t = 3.2 s
(3 marks)
(ii) What value does this result give for the acceleration, in ms-2, of the cylinder down the slope, assuming the acceleration is constant?
s = ut + ½ at2
where u = 0,
therefore acceleration a = 2s/t2
a = (2 x 2.5)/(3.2)2
a = 0.49 m s-2
(2 marks)
(Total 11 marks)







