Capacitor Questions
Q6. A capacitor, initially charged to a pd of 6.0V, was discharged through a 100 kΩ resistor.
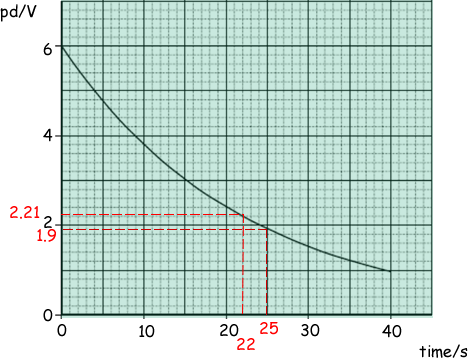
A datalogger was used to record the pd across the capacitor at frequent intervals. The graph shows how the pd varied with time during the first 40 s of discharge.
(a)
(i) Calculate the initial discharge current.
V = IR
I = V/R = 6.0/(100 x 103)
I = 6.0 × 10-5 A 
(1 mark)
(ii) Use the graph to determine the time constant of the circuit, giving an appropriate unit.
Therefore the time constant is time for V to fall to e-1 [or 0.368] of the initial value
The pd will fall to (6.0/e) = 2.21 V when t =time constant
Reading from the graph gives a value for the time constant of 22 (± 1) s
(ΩF is technically correct but not acceptable for the 'unit' mark)
(4 marks)
(iii) Hence calculate the capacitance of the capacitor in microfarads.
time constant = CR
C = 22/(100 x 103)
C = 2.2 × 10-4 F
C = 220 µF
(1 mark)
(iv) Show that the capacitor lost 90% of the energy it stored originally after about 25 s.
Energy = ½ CV2
so, energy ∝ V2
At 25s pd is 1.9V (see graph)
Therefore V2 drops from 62 to 1.92 = 36 to 3.61 = a drop of 32.4
32.4/36 = 0.9 - 90%
OR
when t = 25 s, V2 = 1.9 V from graph
final energy stored = ½ × 2.2 × 10-4 × 1.92 = 3.97 × 10-4 J
and initial energy stored = 3.96 × 10-3 J
which is 10 × greater, so 90% of initial energy has been lost
(3 marks)
(b) In order to produce a time delay, an intruder alarm contains a capacitor identical to the capacitor used in the experiment in part (a). This capacitor is charged from a 12V supply and then discharges through a 100 kΩ resistor, similar to the one used in the experiment.
(i) State and explain the effect of this higher initial pd on the energy stored by this capacitor initially.
The initial energy stored will be four times greaterbecause energy ∝ V2 (and V has been doubled)
(2 marks)
(ii) State and explain the effect of this higher initial pd on the time taken for this capacitor to lose 90% of its original energy.
The time to lose 90% of energy is unchanged because the time constant is unchanged (or it depends only on R and C)
(1 mark)
(Total 12 marks)
About this site
