Capacitor Questions
Q5.
(a) Define the capacitance of a capacitor.
Capacitance is the charge (stored) 
per unit potential difference
C = Q/V
Q = charge (stored by one plate) V = pd (across plates)
(2 marks)
(b) The circuit shown below contains a battery, a resistor, a capacitor and a switch.
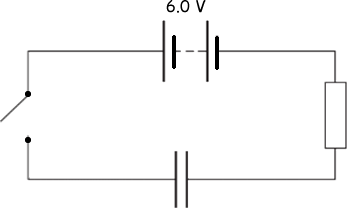
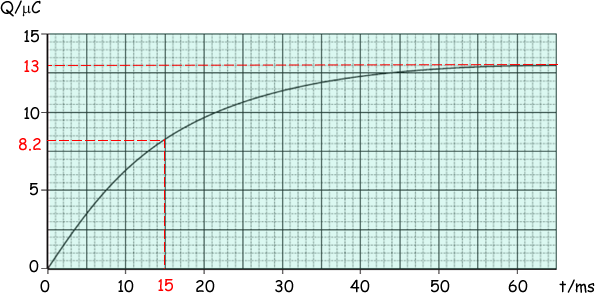
The switch in the circuit is closed at time t = 0. The graph shows how the charge Q
stored by the capacitor varies with t.
(b)
(i) When the capacitor is fully charged, the charge stored is 13.2μC. The electromotive force (emf) of the battery is 6.0V. Determine the capacitance of the capacitor.
C = Q/V
C = 13.2 × 10−6 / 6.0
C = 2.2 × 10–6 F (or 2.2μF)
(3 marks)
(ii) The time constant for this circuit is the time taken for the charge stored to increase from 0 to 63% of its final value. Use the graph to find the time constant in milliseconds.
Q = 0.63 × 13.2 = 8.3 (μC)
(OR Q = 0.63 × 13(.0) (from graph) = 8.2 (μC))
The second mark should show evidence that it was a reading from graph giving time constant = 15 (± 1) ms
(2 marks)
(iii) Hence calculate the resistance of the resistor.
Time constant = RC
R = (15 × 10−3) / (2.2 × 10−6) = 6820 Ω
(1 mark)
(iv) What physical quantity is represented by the gradient of the graph?
gradient = ΔQ/Δt = current
(1 mark)
(c)
(i) Calculate the maximum value of the current, in mA, in this circuit during the charging process.
V = IR
maximum current = maximum voltage/ resistance
I = 6.0/6820
I = 8.8 x 10-4 A
I = 0.88 mA
Or the value from initial gradient of graph: 0.70 – 1.00mA was allowed for this approach
(1 mark)
(ii) Sketch a graph on the outline axes below to show how the current varies with time as the capacitor is charged. Mark the maximum value of the current on your graph.
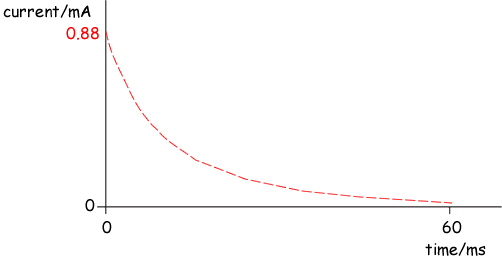
The curve has to start at the value calculated for Imax. This must be marked on the Y-axis.
The line has a decreasing negative gradient and the line is asymptotic to the time axis and approaches ≈ 0 by t = 60ms
(2 marks)
(Total 12 marks)
About this site
