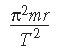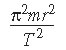Q1. A young child of mass 20 kg stands at the centre of a uniform horizontal platform which rotates at a constant angular speed of 3.0 rad s–1. The child begins to walk radially outwards towards the edge of the platform. The maximum frictional force between the child and the platform is 200 N. What is the maximum distance from the centre of the platform to which the child could walk without the risk of slipping? The frictional force must supply a force equal and opposite to the centripetal force for the child not to slip. Once it cannot equal that force she will fall. mv2/r = m r =200/ m
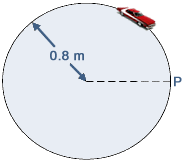
Q2. A model car moves in a circular path of radius 0.8 m at an angular speed of What is its displacement from point P, 6.0 s after passing P? Full circle is 2 In 6 seconds it will have done one and a half. It will therefore be directly opposite point P - a diameter away.
Q3, What is the value of the angular velocity of a point on the surface of the Earth? distance travelled by a point on the Earth's surface in one day = 2 time taken for that is 24 x 602s Therefore velocity v = (2
= (2 We didn't need the radius of the Earth at all as it cancelled - advantage of using symbols and not being too hasty to put numbers in! - but if you wanted it you can get it from your data sheet: the radius of the Earth is 6.37 x 106 m
Q4. A mass on the end of a string is whirled round in a horizontal circle at increasing speed until the string breaks. The subsequent path taken by the mass is:
When released it goes off at a tangent to the circle... as if it had been thrown horizontally. Gravity affects its verical velocity - acceleration in the vertical direction; it goes at constant velocity in the horizontal direction. It therefore follows a parabolic path when viewed in a verical plane.
Q5. A particle of mass m moves in a circle of radius r at uniform speed, taking time T for each revolution. What is the kinetic energy of the particle?
Length of path is 2
Q6. The diagram shows a disc of diameter 120 mm that can turn about an axis through its centre. The disc is turned through an angle of 30° in 20 ms. What is the average speed of a point on the edge of the disc during this time? Always think first about the data you are given - and change it into the form you need to answr the question! Angular velocity is measured in radians - therefore we need to change the 30o into radians. 360o = 2 30o = the time for it to turn 30o is given in millseconds for angular velocity we need to divide we are given a diameter of 120 mm - we need radius for the calculation - in metres! r = 60mm = 60 x 10-3 m
so, v =
Q7. For a particle moving in a circle with uniform speed, which one of the following statements is correct?
Q8. A particle travels at a constant speed around a circle of radius r with centripetal acceleration a. What is the time taken for ten complete rotations? Now, a = Also note that T = time period = 1/f - andt So, a = 4 and therefore T2 = 4 and T= 2 However - we want 10T = 20
Q9. The wheel of the London Eye has a diameter of 130 m and can rotate at a steady speed, completing one rotation every 30 minutes. What is the centripetal acceleration of a person in a capsule at the rim?
In 30 minutes it travels around a circular path - 2πr - you are given the diameter r = 130/2 = 65 m Speed = 2πr/(30 x 60) = 2π x 65 / 1800 = 0.227 ms-1 centripetal acceleration = v2/r = 0.2272/65 = 7.9 x 10-4ms-1
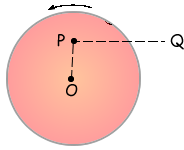
Q10. A small mass is placed at P on a horizontal disc which has centre O. The disc rotates anti-clockwise about a vertical axis through O with constant angular speed.
Which one of the following describes the force which keeps the mass at rest relative to the disc?
Friction is the force that is is holding the mass in a circular path. It therefore is acting towards the centre of the circle.
Q11. A fairground roundabout makes nine revolutions in one minute. What is the angular speed of the roundabout?
9 revolutions per minute = 9/60 per second. 1 rev = 2π radians ∴ angular speed = 2π x 9/60 = 0.94 rad s–1
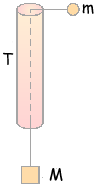
Q12. The figure shows a smooth thin tube T through which passes a string with masses m and M attached to its ends. Initially the tube is moved so that the mass, m, travels in a horizontal circle of constant radius r, at constant speed, v. Which one of the following expressions is equal to M?
The tension in the string is due to the centripetal force of the mass = mv2/r This is balanced by the weight of the mass Mg ∴Mg = mv2/r so M = mv2/rg
Q13. What is the angular speed of a point on the Earth's equator?
Time for full rotation of 2π radians is 602 x 24 seconds in one second: 2π/86400 = 7.27 x 10-5 radians/second
Q14. For a particle moving in a circle with uniform speed, which one of the following statements is correct?
Q15. An object moving at constant speed in a circle experiences a force that is
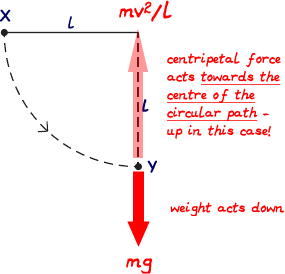
The force keeping an object moving in a circular path is the centripetal force. It acts towards the centre of the circle - at right angles to the movement. Q16. A ball of mass m, which is fixed to the end of a light string of length l, is released from rest at X. It swings in a circular path, passing through the lowest point Y at speed v.
If the tension in the string at Y is T, which one of the following equations represents a correct application of Newton's laws of motion to the ball at Y?
The tension in the string pulls at the mass. The centripetal force of the mass's circular motion is provided by the tension in the string. If we ignore weight then: T = mv2/l When it is in the position shown in the digram, the weight of the mass also produces tension in the string so T = mv2/l + mg This rearranges to give solution C. Q17. A disc of diameter D is turning at a steady angular speed at frequency f about an axis through its centre.
What is the centripetal force on a small object O of mass m on the perimeter of the disc?
acceleration = and So, a = 2 F = ma = 2 Q18. What is the angular speed of a car wheel of diameter 0.400 m when the speed of the car
is 108 kmh–1 ?
On turn of wheel makes the car travel π x 0.400 m. Therefore the wheel turns 108 x 103/ (π x 0.400) times in one hour and 108 x 103/ (π x 0.400 x 602) times in one second. One complete turn is 2π radians, therefore in one second it turns: 108 x 103 x 2π / (π x 0.400 x 602) = 216 x 103 / ( 0.400 x 602) = 150 rads - choice B
|
Follow me...
|