Nuclear Fission
Q1.
(a) The mass of a nucleus is M.
(i) If the mass of a proton is mp, and the mass of a neutron is mn, give an expression for the mass difference ∆m of this nucleus.
∆m = Zmp + (A – Z)mn – M 
(ii) Give an expression for the binding energy per nucleon of this nucleus, taking the speed of light to be c.
Eb = ∆mc2/A 
(2 marks)
(b) The figure below shows an enlarged portion of a graph indicating how the binding energy per nucleon of various nuclides varies with their nucleon number.
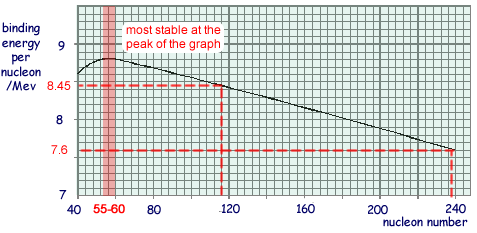
(i) State the value of the nucleon number for the nuclides that are most likely to be stable. Give your reasoning.
Any value of A in range 54 → 64 gets you the mark.
Reasoning: Stability increases as binding energy per nucleon increases as more energy is required to pull each of the nucleons apart. 
(ii) When a fission of uranium 235 takes place so that the nucleus splits into two roughly equal parts and approximately 200 MeV of energy is released. Use information from the figure above to justify this figure, explaining how you arrive at your answer.
Binding energy per nucleon increases from about 7.6 MeV to 8.45 MeV  - an increase of about 0.85 MeV.
- an increase of about 0.85 MeV.
Therefore for 235 nucleons the energy will increase by 235 x 0.85 
= 200 MeV in total 
(5 marks)
(Total 7 marks)


