Q16.

(a) The concept of an absolute zero of temperature may be explained by reference to the behaviour of a gas. Discuss one experiment that can be performed using a gas which would enable you to explain absolute zero and determine its value.

It is not necessary to give full details of the apparatus.

Your answer should:

include the quantities that are kept constant

identify the measurements to be taken

explain how the results may be used to find absolute zero

justify why the value obtained is absolute zero.

[6 marks]

High Level – Good to Excellent

An experiment with results and interpretation must be given leading to the measurement of absolute zero. The student refers to 5 or 6 points given below. However each individual point must stand alone and be clear. The information presented as a whole should be well organised using appropriate specialist vocabulary. There should only be one or two spelling or grammatical errors for this mark.

Intermediate Level – Modest to Adequate

An experiment must be given and appropriate measurements must be suggested. For 3 marks the type of results expected must be given. 4 marks can only be obtained if the method of obtaining absolute zero is given. The grammar and spelling may have a few shortcomings but the ideas must be clear.

Low Level – Poor to Limited

One mark may be given for any of the six points given below. For 2 marks an experiment must be chosen and some appropriate results suggested even if the details are vague. Any 2 of the six points can be given to get the marks. There may be many grammatical and spelling errors and the information may be poorly organised.

A competent answer should include:

The experiment uses a constant mass of gas (this fact may be clear from the experiment description saying that the gas is trapped) and constant volume (or constant pressure).

The experiment must involve changing the temperature with pressure or volume being the dependent variable. Pressure (or volume) must be recorded for a range of temperatures.

How the temperature is maintained/changed/controlled. (The gas must be heated uniformly by a temperature bath or oven – not by radient energy from an electric fire or lamp)

Describe how a graph of pressure against temperature (or volume against temperature) produces a straight line graph OR reference to the Pressure Law or Charles' Law.

How the line can be extrapolated to give a temperature of absolute zero at zero pressure (or volume), which is at 0 K or -273 ^oC.

An explanation of particle behaviour - Absolute zero is obtained using any gas (provided it is ideal or not at high pressures or close to liquification) Or Absolute temperature is the temperature at which the volume (or pressure or mean kinetic energy of molecules) is zero/or when the particles are not moving.

(b)

(i) State two assumptions about the movement of molecules that are used when deriving the equation of state, pV = – ¹/₃ N m (c_^rms)² for an ideal gas.

Any two from:

The motion of molecules is random.

Collisions between molecules (or molecules and the wall of the container) are elastic.

The time taken for a collision is negligible (compared to the time between collisions)

Newtonian mechanics apply (or the motion is non-relativistic).

The effect of gravity is ignored or molecules move in straight lines (at constant speed) between collisions.

If more than 2 answers were given each wrong statement cancelled a correct mark - sometimes they just take the first two answers, sometimes they use additional incorrect information to cancel marks you have gained - it is best to just give what you are asked for!

[2 marks]

(ii) Three molecules move at the speeds shown in the table below:

molecule	speed / m s–1
1	2000
2	3000
3	7000

 

Calculate their mean square speed.

mean square speed = (2000² + 3000² + 7000²) / 3

mean square speed = 2.1 x 10⁷ m² s ^-2

Even though the numbers look to be 1sf - never give answers to 1sf - 2 sf minimum....

[3 marks]

 

(c) The average molecular kinetic energy of an ideal gas is 6.6 × 10^–21 J.

Calculate the temperature of the gas.

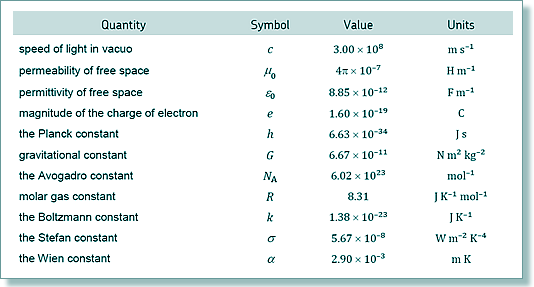
mean KE = 3RT/(2N_A) ( or you can substitute into mean KE = 3kT/₂)

T = 2N_A x mean KE / 3R

T = 2 x 6.02 x 10^{23 x} 6.6 x 10^-21/(3 x 8.31)

T = 320 K

[3 marks]

(14 marks total)