A level: Kinetic Theory Questions
Q1. A single gas molecule of mass m is moving in a rectangular box with a velocity of ux in the positive x-direction, as shown in the diagram. The molecule moves backwards and forwards in the box, striking the end faces normally and making elastic collisions.
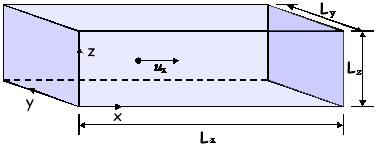
(a)
(i) Show that the time, t, between collisions with the shaded face, is:
t = 2Lx/ux
molecule travels 2Lx 
between collisions at a velocity of ux,
v = s/t
and so, t = s/v
s = 2Lx
v = ux
t = 2Lx/ux
(ii) In terms of m and ux write down an expression for the change of momentum per collision with the shaded face.
change of momentum per collision = 
p
= mux - (-mux) = 2mux
(2 marks)
(b) If it is assumed that the box contains N identical molecules, each of mass m, all moving parallel to the x-direction with speed ux and making elastic collisions at the ends, show that the average force, F, on the shaded face is given by
F = Nmux2/Lx
force for one mlecule = rate of change of momentum of one molecule
p/t = (2mux )/(2Lx/ux)
=mux2)/Lx
for N molecules the force will be = Nmux2)/Lx
(2 marks)
(c) In a better model of molecular motion in gases, molecules of mean square speed are assumed to move randomly in the box.
(i) By considering this random motion obtain an expression for ux2in terms of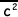 
For a typical molecule with a velocity u, the velocity can be written as a sum of its vector components:
u2 = ux2 + uy2 + uz2
When dealing with a large number of molecules the mean square value of movement vectors of the molecules with totally random motion will show no preferred direction, therefore:
and 
(ii) Show that a better expression for F is
F = Nm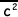/(3Lx)
and
therefore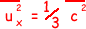 
Substituting into the equation F = Nmux2/Lxwe get:
F = Nm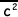/(3Lx)
(iii) Hence derive the equation pV = 1/3 Nm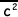
pressure = force/area
Force = Nm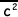/(3Lx)
area = LyLz
pressure = Nm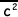/(3LxLyLz)
but volume V = LxLyLz
so, pV = 1/3 Nm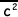
(5 marks)
(Total 9 marks)
About this site
