'O' Level Standard Questions - Refraction Q10.
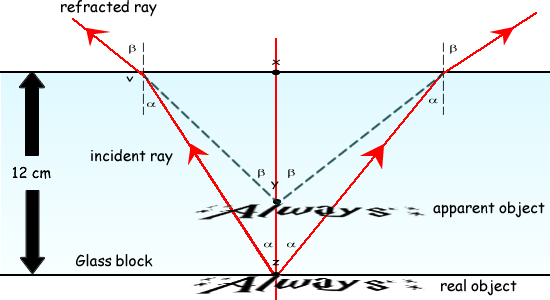
Snell's Law: nairsin θair= nglasssin θglass
1 x sin β = nglassx sin α ∴ nglass= sin β/sinα = real depth/apparent depth 1.50 = 12/apparent depth apparent depth = 12/1.5 = 8.0 cm = distance xy The distance the ink has apparently risen = distance xz - distance xy = 12 - 8.0 = 4.0 The ink is therefore apparently raised 4.0 cm into the block
|
Follow me...
|