Accuracy and Precision

Presenting Results in a table

Tables should always be used to present results.

There should be a column for

each set of readings taken (never omit these!)

each set of calculated values from the experimental data (these may be derived for you to calculate values or plot a graph)

Headings should

be at the top of a column of numbers (this is preferable to on the left of a series of results).

give the physical quantity measured in words (eg. current, potential difference, length, time) . Abbeviations (I, V, l, t) can be used only if it is clear what they stand for in the text - it is best to include both!

include the unit the physical property is measured in. This should preferably be the S.I. unit (as this is the one that will be required in calculations).e.g. Current I (A)

have an indication of the error involved in taking the reading (if applicable). This can be given as a + value or percentage

have border lines drawn around them.

Columns should

contain only numerals (Your units are at the top already.... it would be a mistake to put them in again!)

contain numbers to the correct number of significant figures. This should indicate the accuracy to which you can read the instruments you have used. (e.g. 0.20 m indicates a reading taken to the nearest cm whereas 0.2 cm indicates you can only read to the nearest 10 cm and 0.200 m to the nearest mm). Therefore a column representing a set of readings taken with the same instrument should all have the same number of significant figures.

have border lines drawn around them

Word-processing of results can lead to errors. You should be very careful to check your final draft carefully if you word process a report!

Common errors that lose you marks:

Using the wrong font: remember the symbol allows you to put in greek letters such as W, n, and m.

Entering numbers to the wrong number of significant figures (especially if worked out on a spreadsheet without thought to formatting the numbers in the column).

Missing out the columns for 'readings taken' - only including columns needed to calculate the conclusion value or plot a graph is a major error - you must include the columns of results you took during the experiment!

Incorrectly calculated derived values because you have put the wrong formula into your spreadsheet - always check at least two values in a 'fill down' column with your calculator!

Not drawing a border - making it a list of numbers not a table of results.

Significant Figures

In experimental physics significant figures in a number refers to all the figures obtained by direct measurement, excluding any zeros which are used only to place the decimal point.

e.g.

When numbers are used in calculations then the number of significant figures in the answer should be found by using an analysis of error measurements. This is because the last significant figure tells the reader to what precision you are recording the value.

e.g.

Therefore if we have values of 0.96 and 1.25 which are to be multiplied we are claiming the precision of each number is ;

0.5 % for 0.96 0.4% for 1.25

Hence 0.96 x 1.25 = 1.2 but this implies a precision of 4% and therefore we would be better to write 1.20.

As a general rule when multiplying or dividing numbers express your answer to the same number of significant figures as the least precise figure.

e.g. (i) 2.4 x 33.5 = 80.4

least precise figure is 2.4 with 2 significant figures and hence we write the answer as 80

e.g. (ii) 18.5 - 0.9300 = 19.892473

least precise figure is 18.5 with 3 significant figures and hence we write the answer as 19.9 (notice that when the answer is rounded off to three significant figures if the fourth figure is five or greater the third would increase by 1 but if it were four or less then it would stay the same).

Accuracy and Precision

As with many ideas in science accuracy and precision often cause problems not because they are difficult to understand but because they have 'everyday' and 'scientific' meanings. You need to have a scientific understanding of the two terms if you are to gain maximum credit for your work.

Accuracy

This refers to results that are close to the 'actual value'. We say that the systematic error is very small.

Precision

This refers to the spread of repeated results. We say that the random error is very small if they are close to each other

Does one imply the other?

Simply put the answer to that must be 'no' since data can be:-

• accurate and precise
• inaccurate and precise
• accurate and imprecise
• inaccurate and imprecise

e.g. 1. Measuring the diameter of a sphere to be used in a terminal velocity investigation. If the true value of the diameter is 1.00 cm and you use a micrometer reading to 0.0005 cm then the precision would be ± 0.05%. However if the micrometer has a large zero error then the data would be inaccurate.

e.g. 2. If you measure the diameter of the same sphere but this time use a metre rule
calibrated in mm you could estimate to the nearest 0.5 mm which gives a precision of ± 5%. However you are likely to have a mean value which is very close to the actual value which makes the data accurate.

Dealing with Errors

Errors in a single measurement

Errors in a large number of measurements of the same quantity

Errors in derived data

Adding or subtracting quantities

Multiplying or dividing quantities

Raising a number to a power
 
 

Here we are dealing with the quantifiable errors, either random or systematic, which occur during any experimental work. These errors are not to be confused with mistakes. For example, a badly plotted point on a graph or a transcription error when taking data from one table to another is a mistake NOT an error.

Errors in a single measurement

Imagine that some sort of super being was capable of measuring the diameter of a disc as 10.34526765867m. If you or I try to measure the diameter of the same disc, we are limited by our ability to read the instrument being used and the smallest division on that instrument. If we record the diameter to be 10.345m we are saying that it lies between 10.344 5m and 10.3455m that is an error of ±0.000 5m.

The value would then be recorded as 10.345 ± 0.0005 m.

Errors in a large number of measurements of the same quantity

When a number of repeat readings are taken then fluctuations due to the ability of the observer and the limitation of the apparatus can be shown and an estimation of the error made.

Imagine that the following measurements were made for the diameter of a wire with a standard wire gauge of 36.

0.220mm, 0.201mm. 0.190mm. 0.190mm, 0.190mm. 0.191mm. 0.190mm. 0.200mm. 0.191mm. 0.195mm.

First find the mean value, add up all the values and divide by the number of values, this gives a value of 0.1958mm.

To calculate the error we need to calculate the absolute, i.e. ignore any negative signs, difference between the mean value and each individual value. This is the deviation from the mean and the error estimate is the mean of these deviations. A spreadsheet can easily be set up to do this for you.

For our values we get a mean deviation of 0.006720. Since this value is an estimation it is a good idea to keep a careful eye on the number of significant figures. In this instance the value would be best recorded as;

Errors in derived data

Once readings have been recorded they are usually put into some formula or equation to generate what is called derived data. We cannot know if the error in the individual quantities are going to cancel each other or compound each other. To be sure we take the more pessimistic of the two. To calculate these errors simple formulae can be used.

Adding or subtracting quantities

When adding or subtracting quantities the combined error is found by adding the absolute error.

If c = a + b or c = a - b and the absolute errors in a and b are ± =Δa and ±Δb

then Δc = Δa + Δb where Δc is the absolute error in c

e.g. The four sides of a soccer pitch are measured to be 75.1m. 75.9m, 33.2m and 33.7m each with an error of ± 0.1 m. The perimeter of the pitch is then 217.9 ± 0.4m

Multiplying or dividing quantities

When multiplying or dividing quantities the combined error is found by adding the percentage or fractional error.

If c = a x b or c = a/b and the percentage errors in a and b are ± Da/a and ± Db/bthen Dc/c = Da/a + Db/b where Dc/c is the percentage error in from which Dc the absolute error in c can be calculated. e.g.

A current of 5.0 A which is read to a precision of ± 0.1A flows through a resistor of nominal value 1000. The resistor is said to be accurate to ± 10%. The potential difference across the resistor would be found by;

The percentage error in the value of V would be found by

Raising a number to a power

If we raise a number to a power it is a special case of multiplying a number by itself and you can easily show that if the percentage error in z is ± Dz / z then the error in z² is ± 2Dz /z. In general we can say that if the percentage error in z is ± Dz then the percentage error in zⁿ is nDz / z where n is a positive number.

e.g. If the mean value for the diameter, d, of a wire is 0.194 ± 0.004mm then the cross-sectional area, A can be found from:
A = pd² / 4
A = (3.142 x O.194² ) /4 = 0.0296 mm²

The easiest way to work out the error is to work out the max and min of the value…

MAX diameter is 0.198 mm
Therefore A(max) is 0.0308 mm²

Similarly MIN diameter is 0.190 mm
Therefore A(min) is 0.0284 mm²

Error is therefore +0.0012 mm²

So the percentage error is (0.0012/0.0296) x 100 = 4.1%

Alternatively you can argue that:

The percentage error in A is equal to the percentage error in d²

Dd² /d = 2Dd /d (two lots because it is squared!) = 2 x 0.004 / 0.194 = 0.0412
= 0.0412 x 100% = 4.12%

Therefore A / A = 0.0412
Which gives A (the absolute error in A) = 0.0012 mm²

Therefore we record A = 0.0296 ± 0.0012 mm²

Using Graphs

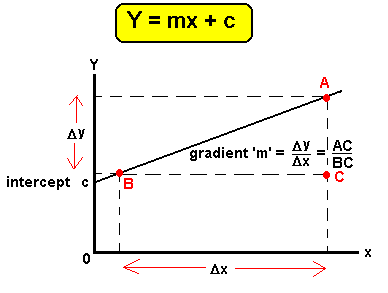
The general form of a linear equation is y = mx + c in which y is taken to be the dependent and x the independent variable; this is the one that you vary. with m and c being constants. The gradient of the line. which may be negative, gives the value of m whilst the intercept on the vertical axis gives the value of c.

A graph is used to summarise data in a pictorial way such that the main features of the relationship under investigation can be seen. Since linear relationships are easier to 'see' the straight line graph is of great importance in physics.

Plotting graphs

In order to extract the maximum of reliable data from a graph it is important to make full use of the graph paper,

a. Whenever it is available make use of 1mm A4 graph paper but in all case use A4 graph paper

b. When choosing a scale for the graph ensure your data covers at least 8cm by 8cm on that scale

c. When finding the gradient make sure that you use the largest possible values for Δx and Δy.

d. Include error bars and / or least and greatest gradient lines

e. Do not forget the units for m and c

The intercept

For an equation of the form y = mx + c when x = 0 then y must be equal to c

Sometimes in order to generate a more sensible scale it is better not to start at x = 0 but the above warning must then be remembered. The y-axis does not, however, need to start at y = 0 in order to obtain the value of c from the intercept

The gradient

If we consider the equation y = mx + c then we can transpose to give;

You should also notice that the gradient is given by

OR

Not all of the relationships you investigate will be linear in nature, many will be of the form y = kxⁿ where k and n are constants. Plotting a graph of y and x would produce a curve which would not allow k or n to be found. This can be resolved be the use of logs.

So, if you now plot log y on the vertical axis and log x on the horizontal a straight line will be produced which will allow 'n' to be found from the gradient and log k to be found from the intercept. This, in turn, allows k to be found.

When you plot a log graph the log values need to be tabulated; note that log values do not have units.
 

Rather than draw a log graph to turn a curve into a straight line it is sometimes useful to use a curve in order to more readily see the trend of the results. Information is sometimes required that means finding the gradient of the curve at a given point. This is done by drawing a tangent to the curve at that point A tangent only touches the curve at that one point and is said to be 'perpendicular to the normal of the curve at that point'

Drawing tangents is often utilised in work involving varying rates.

Dealing with Errors when Using Graphs

When a graph of the form y = mx + c is plotted it produces a straight line. The gradient of such a graph is m and the intercept c. These values are often the quantities we are trying to find in our investigation and as such some estimation of the error in them needs to be made.

The best fit line is used to give a measurement of the gradient and intercept. This must be shown in your coursework. However if we wish to estimate the error then we can draw the two additional lines -one the steepest possible through the points and one at the shallowest gradient. The gradient of the steeper of the two is called M_max and the other M_min.

The error in the value of m can be estimated as Dm = (M_max - M_min )/2 Therefore the value quoted for the gradient is m ±Dm

The error in the intercept can be treated in the same way giving Dc = (c_max - c_min )/2

Hence this value is recorded as c ± D c

Obviously you need to keep a careful eye on the number of significant figures used and also try to make sure that you don't include any points which are known to be in error, If a point seems to be too far away from the trend shown by the others either go back and check it or consider leaving it out. If you leave it out of your graph you should still record it in your results table and comment on why you have omitted it from the graph.

The values for the quantities on the x and y axes will have an error associated with them and this can be shown on the graph by the use of error bars. Rather than simply plotting a point lines are added to show the error range.