Consider a point pendulum bob connected to a massless rope or rod that is held at an angle q from the horizontal. If you release the mass, then the system will swing to a position at an angle q from the horizontal on the other side and back again to its starting position. This is one full period of the swing.

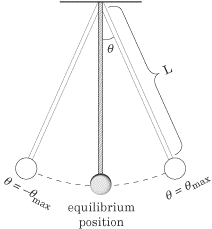
It can be determined that:

where

• T is the period, or time for one complete swing,
• l is the length - the distance from the point of suspension to the center of gravity of the bob. Care has to be taken that the point of suspension is a point - this can be achieved by clamping the string frimly between two pieces of card.
• g is the acceleration of gravity.

Forces acting on the pendulum

When you release the pendulum bob it will accelerate toward the equilibrium position. As it passes through the equilibrium position, it will slow down until it reaches a position - , and then accelerate back. At any given moment, the velocity of the pendulum bob will be perpendicular to the rope. The pendulum’s path follows an arc of a circle, where the rope is a radius of the circle and the bob’s velocity is a line tangent to the circle.

To calculate the forces acting on the pendulum at any given point in its trajectory it will be most convenient to choose a y-axis that runs parallel to the rope. The x-axis then runs parallel to the instantaneous velocity of the bob so that, at any given moment, the bob is moving along the x-axis.

Two forces act on the bob:

• the force of gravity, F = mg, pulling the bob straight downward and
• the tension of the rope F_T pulling the bob upward along the y-axis.

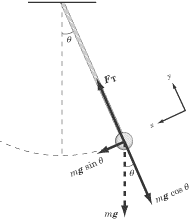
The gravitational force can be broken down into an x-component, mg sin 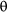, and a y-component, mg cos.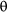

The y component balances out the force of tension—the pendulum bob doesn’t accelerate along the y-axis—so the tension in the rope must also be mg cosQ.

Therefore, the tension force is maximum for the equilibrium position and decreases with .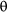

The restoring force is mg sin 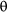, so the restoring force is greatest at the endpoints of the oscillation, and is zero when the pendulum passes through its equilibrium position.

N.B. The restoring force for the pendulum, mg sin 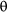, is not directly proportional to the displacement of the pendulum bob which makes calculating the various properties of the pendulum very difficult. Pendula, however, usually only oscillate at small angles, where sin = 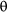(in radians). In such cases, we can derive straightforward formulae, which are only approximations but work well enough in practice.

Click here to consider the energy transitions