|
Nuclear
equations can be used to show the decay process.
When you studied at 14-16 you learned that
these must balance for nucleon number and proton number. Now at 16+
baryon number, charge and lepton number must balance too.
 Example of Alpha Decay
Example of Beta Decay
Example of Positron
Decay
Example of Gamma Emission
Alpha decay
A nucleus that has high mass and too many
protons to be stable tends to undergo alpha decay.
When alpha decay occurs a group of two
protons and two neutrons (helium nucleus) comes out of the nucleus.
Therefore the proton number decreases by 2 but the nucleon number decreases
by 4. The resulting daughter nucleus is of an element 2 positions to
the left of the 'parent' in the periodic table.
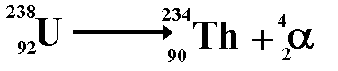
The above equation shows the radioactive
decay of Uranium-238 by alpha emission.
Look at the numbers on the top line (the
nucleon numbers). Each nucleon has a baryon number of 1/3 therefore
79.3 = 78 + 1.3
Look at the numbers on the bottom line
(the proton numbers) - indicate charge of +1 for each proton number.
92 = 90 + 2
The decay does not involve leptons therefore
this is zero each side.
Beta Decay
When a nucleus has too many neutrons, it
tends to beta decay.
When beta decay occurs a neutron within
the nucleus emits the particle and changes into a proton. Therefore
the proton number increases but the nucleon number stays the same (only
now you have one more proton and one less neutron!). The resulting daughter
nucleus is of an element 1 position to the right
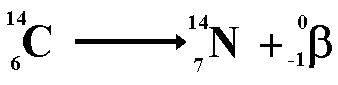
The above equation shows the radioactive
decay of Carbon-14 by beta emission.
Look at the numbers on the top line (the
nucleon numbers) each of these has a baryon number of one third ...
4.6 = 4.6 + 0
Look at the numbers on the bottom line
each representing charge.
6 = 7 + (-1)
However when we look at the lepton numbers
we have an imbalance
On the left of the equation we have no
leptons therefore the lepton number is zero.
On the right of the equation we have a
'matter lepton' (the electron) giving a lepton number of +1
We therefore need to add an anti-matter
lepton (lepton number -1) to the right. The anti-lepton must not disturb
the balance of charge or of baryon number. The candidate for this task
is the anti-neutrino.
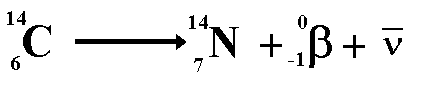
Positron Decay
When a nucleus has too many protons, it
tends to positron decay. A positron is an antimatter beta particle.
When a positron meets with an electron it annihilates it! Both particles
disappear and two gamma rays are produced instead.
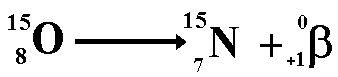
The above equation shows the radioactive
decay of Oxygen-15 by positron emission
Look at the numbers on the top line (the
nucleon numbers) each of these has a baryon number of one third ...
5 = 5 + 0
Look at the numbers on the bottom line
(the proton numbers).
8 = 7 + 1
However when we look at the lepton numbers
we have an imbalance
On the left of the equation we have no
leptons therefore the lepton number is zero.
On the right of the equation we have an
'anti-matter lepton' (the positron) giving a lepton number of -1
We therefore need to add a matter lepton
(lepton number +1) to the right. The lepton must not disturb the balance
of charge or of baryon number. The candidate for this task is the neutrino.
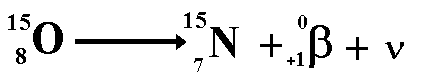
This now balances on all counts!
Gamma
Emission
Sometimes, after its emission of an alpha,
beta or positron particle, the nucleus is still in an excited state,
called a metastable state. In order to get to a lower energy state it
emits a quantum of energy in the form of a gamma ray. This is not a highly unstable state otherwise the emission of the gamma ray
would accompany the alpha, beta or positron particle. Nuclei in the
metastable state produce gamma rays at a measurable half-life.
E.g. Cobalt 60m decays to give cobalt 60
with a half-life of 5.3 years and technetium 99m decays to give technetium
99 with a half-life of 6 hours.
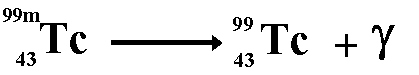
No matter is emitted from the nucleus therefore
the nucleon number and the proton number remain the same. Before and
after emission of the gamma ray they are the same isotope of the element
but they are different nuclide because the term nuclide incorporates
nuclear energy states as well basic structure.
|
Nuclear
Equations 
