Carbon - 14

If the equilibrium concentration of carbon 14 in living plants gives 16 disintegrations per minute per gramme of carbon, estimate the age of a piece of timber if 2.0g of carbon prepared from it gives 15 disintegrations per minute. (The half-life of carbon 14 is 5.57 x 10³ years.)

14g carbon 14 contains N_A atoms

therefore a 2g sample contains (6.02 x 10²³) / 7 atoms

N = (6.02 x 10²³ ) / 7

half-life = 5.57 x 10³ years

= 5.57 x 10³ x 365.25 x 24 = 4.88 x 10⁷ hours

= 2.93 x 10⁹ minutes

l = ln2/half-life = 0.693 / 2.93 x 10⁹ = 2.37 x 10^-10 minutes ^-1

dN/dt = -lN

Age is zero when dN/dt = 16 min^-1 g^-1

Age is t when ^dN/dt = 15 min^-1 for a 2g sample = 7.5 min^-1 g^-1

the ratio of ^dN/dt to N is constant therefore 16/N₀ = 7.5/N_t

and N_t /N₀ = 7.5/16

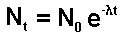
So,

e^-lt = 7.5/16

Taking logs

-lt = ln (7.5/16)

t = -ln(7.5/16)/l

t = 0.758/(2.37 x 10^-10)

=3.2 x 10⁹ minutes

= 6080 years

= 6100 years (2 sig figs)