To investigate the relationship between molecular kinetic energy and temperature

From the kinetic theory of gases:

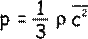
Therefore let us multiply both sides by V to get an expression for any volume V of gas:

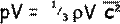
Now

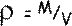
So,

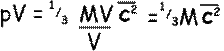
Where M is the total mass of the gas of volume V.

Now, M = Nm ( where m is the mass of one particle in the gas and N is the number of particles in the gas)

So

A bit of mathematical magic can make that last part of the equation represent kinetic energy. To do that we need a ½ factor before the m… to make it fair we have to put a factor of 2 in front of the N:

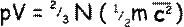
Now the Equation of State or Ideal Gas Equation (which you should know by heart!) is

pV = nRT

where

R = the universal molar gas constant,

T = the temperature in kelvin, and

n = number of moles of gas

We can therefore put:

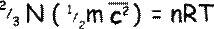
Rearranging the equation we get that:

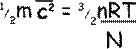
Now, as N/n is the number of molecules per mole, i.e. N_A, the Avogadro constant, so we can get rid of the factors that require us to know the details of the gas and replace them with a constant.

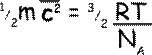
Both R and N A are universal constants, and therefore so also is R/N A; it is called Boltzmann's constant, ‘k’ and it is the gas constant per particle. The left-hand term is the average translational kinetic energy of a single molecule, and therefore

Average translational kinetic energy of a particle of gas = ³/₂kT

Things to remember!

• ‘T’ must be in kelvin – remember to convert!
• The E_k is in joules and is for one average particle – the question often asks you for the energy of a number of moles of gas.