Scalars and Vectors

Scalar quantities have only magnitude (size) but vector quantities have magnitude and direction. For example, the weight of an objects acts down towards the Earth's centre but its mass is just a quantity. Forces can push in different directions but energy has no direction associated with it.

Speed is a scalar quantity and velocity is a vector quantity. Consider the following example. A toy car on a circular track takes 't' seconds to complete half a lap. What is its average speed and what is the magnitude of its velocity? It travels from A to B around the track. The distance it travels is therefore half of the circumference, but its displacement after half a lap is the diameter of the circle. speed = distance travelled/time taken = d/(2t) velocity magnitude = d/t

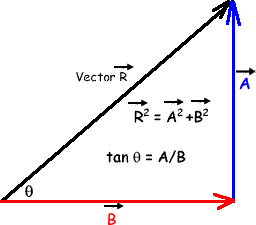
You represent vectors with an arrow - the length of the arrow represents the magnitude of the vector and the direction it points on the page represents the direction.

You usually put a little arrow over the top of the letter representing a vector in your diagrams.  

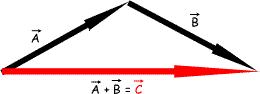
Addition

To add scalars is easy - you just add the values together, but adding vectors is a little more complicated. You have to take the direction into account.

At GCSE you will only have to add co-linear vectors (ones that are in a straight line).

Vectors pulling in the opposite direction simply cancel the effect of the each other out.

At A Level it is a little more complicated. You have to tackle vectors that point in all directions!.

To add them you simple draw them to scale. (Use graph paper - it makes the operation much simpler) You arrange them so that the arrow tail of one vector is at the arrow head of another
You then draw in a vector that goes from the tail of the first vector to the head of the last one. That is your resultant vector. That one vector could replace all of the ones you added together and achieve the same final result.

When drawing out vectors you have to be careful to draw them very carefully.

• Use a sharp pencil
• Use a ruler
• Use a protractor.

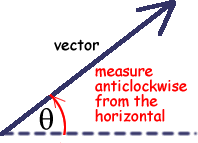
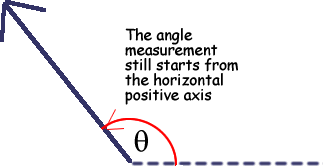
Always put the scale you are using on the paper - for example write 1 cm 10N.(Remember not to put that 1 cm = 10N - length cannot equal force on represent one!) Choose as large a scale as possible - that will make your answer more accurate - If you can measure a line to the nearest mm - then a line 1cm long will have a 10% tolerance but one 10cm long will have a 1% tolerance

The examiners will usually draw a diagram for you and add angles in so that you can do calculations but if the vector is simply written as 20N at 35^o, you need to understand what is meant by that....

The angle of a vector is measured from the horizontal in an anticlockwise direction

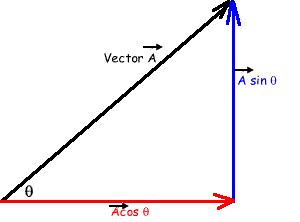
Vector addition by calculation

To add vectors that are pointing in different directions you need to break them down into their horizontal and vertical components. These can then be easily added together to obtain the vertical and horizontal components of the resultant vector. A simple use of Pythagoras Theorem then gives you the magnitude of the vector - and a little bit of 'trig' gets you the angle. It is really simple to do!

First sketch the vector line on your page - you do not need to do it to scale if you are calculating values, but a sketch diagram is always useful. Then make that vector into a right angled triangle (as shown in the diagram) by drawing in two vectors that could replace it - one horizontal and one vertical.
You then need to work out the value of the horizontal and vertical components by using trigonometry. The vector A is the hypotenuse of the triangle. The vertical component is 'the opposite' side of the triangle (it is opposite the angle). The horizontal component is 'the adjacent' side of the triangle - it is adjacent to the angle. Therefore the sine of the angle is the vertical component divided by the vector and the cosine of the angle is the horizontal component divided by the vector: Vertical component = A sin similarly Horizontal component = A cos
You do this with each of the vectors that you have to add together. You then add up all of the vertical components and all of the horizontal ones This gives you a triangle that represents the vector R (the resultant vector).
You can then use Pythagoras Theorem to find the magnitude of the resultant vector and trigonometry to find the angle of the vector (tan of an angle is opposite over adjacent).

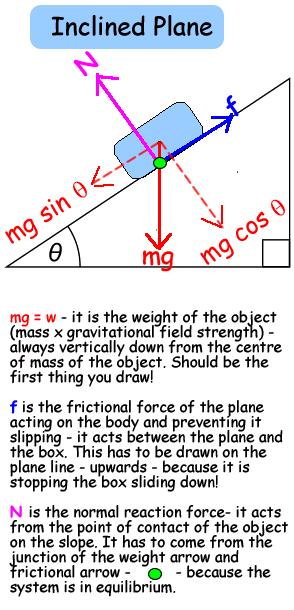
Subtracting vectors

To subtract a vector simple reverse its direction - then add it!

Multiplying vectors by scalars - this affects the magnitude only.

Multiplying vectors by vectors (cross and dot products) - this can affect magnitude and/or direction - it is not required at A level in Physics.

You can practise resolving vectors into their components by using my interactive XL spreadsheet. Try it out! Simply make up a vector (say, 64N at 23 degrees to the horizontal) and then use your calculator to work out the horizontal and vertical components of it. The spreadsheet will tell you if you have done it correctly. Enter the values into the sheet and it will work out the components for you. This is a useful tool for you to use when you need extra practice.

Resolving vectors on an inclined plane

Click here to go to an interactive activity

Click on the above link to find out about inclined planes.... then look at the vidclip below for how to solve a problem relating to one.

Here is a link to the page on three coplanar forces in equilibrium.  

Here is an interactive application