Design of a simple adder/subtactor

	a3	a2	a1	a0
+	b3	b2	b1	b0
	__	__	__	__
	s3	s2	s1	s0

	a3	a2	a1	a0
+	b3	b2	b1	b0
	s3	s2	s1	s0

a0	b0	s0	c1
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

The one bit adder does just that - adds two single bit values together.

The 'c' column is a 'carry' column.

When we add 01 and 01 we get 10 - that single bit value is zero - but we have to carry a value on to the next column.

The S₀ output can be seen to be XOR (only high if a or b is high - not if both are high or both are low.

s₀ = a₀ XOR b₀

c₁ = a₀ AND b₀

C1 output can be seen to be high only when a and b are high so it is an AND relationship. We can now look at the second, and subsequent, columns - but this time there is a 'c' column to take into account too... as we might have to 'carry' a value.

	a3	a2	a1	a0
	b3	b2	b1	b0
+	c3	c2	c1
	s3	s2	s1	s0

This time we have the possibility of a carry-bit from the addition of the LSB column.

a1	b1	c1	s1	c2
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1

s₁ = XOR (a_ib_ic_i) - XOR is high if number of inputs is odd.

c₂ = a₁b₁+ b₁c₁ + a₁c₁

This can be applied to any line of the truth table... so if we replace the number of the bit-line we are examining with 'i' we get:

si = XOR (aibici) ci+1 = aibi+ bici + aici

We can now draw a logic gate diagram for the adder.

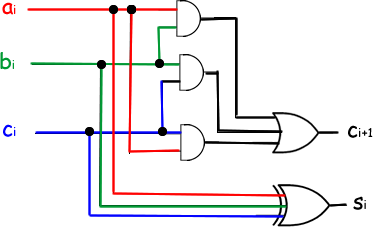
The truth table and the logic gate diagram uses 'i' and 'i+1' etc to be 'general'. You could therefore do any level you were asked to.

For example if 'i' was 3 the values would be:

s₃ = XOR(a₃,b₃,c₃)

c₄ = a₃b₃ +a₃c₃ +b₃c₃