Magnetic Fields - Structured Questions

Q2. The diagram below shows the path of protons in a proton synchrotron.

The protons are injected at a speed of 1.2 × 10⁵ ms^–1 and a magnetic field is applied to make them move in a circular path.

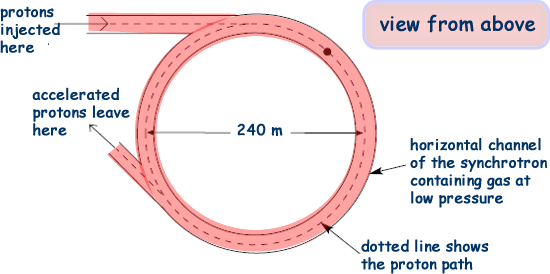
(a) Calculate the magnetic flux density of the field required for protons to move in the circular path when their speed is 1.2 × 10⁵ ms^–1.

The force from the magnetic field F_M = BQv becomes the centripetal force that makes the charged particles move in a circle F_c = mv²/r

∴  BQv = mv²/r

B = ^mv/_rQ

B = 1.67 × 10⁻²⁷ × 1.2 × 10⁵ /(120 x 1 .6 x 10^-19) = 1.04 × 10⁻⁵

B = 1.0 × 10⁻⁵ T

This magnetic field must act upwards, out of the plane of the page (Fleming's left-hand rule)

(b) Explain how the magnetic flux density required to maintain the circular path has to change as the kinetic energy of the protons increases.

In a synchrotron the radius of the path travelled by the charged particles remains constant as they are progressively accelerated. This enables a single particle track to be used, rather than an increasing radius of path as in the cyclotron. For this to be achieved, the increase in magnetic flux density has to be synchronised with the increase in velocity.

As the kinetic energy of the protons increases the radius of the path they take would increase if the magnetic field strength remained steady. The magnetic flux density therefore has to increase because in a path of constant radius (using the same charged particles) magnetic flux density B ∝ v

(5 marks)