Topic Menu

Cyber-chess a chess instruction site

Radioactivity: Multiple Choice Questions

Q1. Which of the following best describes the decay constant for a radioisotope?

A

The reciprocal of the half-life of the radioisotope.

B

The rate of decay of the radioisotope.

C

The constant of proportionality which links half-life to the rate of decay of nuclei.

D

The constant of proportionality which links rate of decay to the number of undecayed nuclei.

 

From the equation you can see that λ links N (number of undecayed nuclei) with ΔN/Δt (the rate of decay)

 

 

Q2. After 64 days the activity of a radioactive nuclide has fallen to one sixteenth of its original value. Calculate the half-life of the radioactive nuclide.

A

2 days.

B

4 days.

C

8 days.

D

16 days.

 

1/2 - 1/4 - 1/8 - 1/16

4 half lives are 64 days so 1 half life is 16 days

 

Q3. Radioactive decay is described as being spontaneous. In this context spontaneous means:

A
 nothing can influence the decay
B
 the decay is random
C
 the decay can be predicted
D
 the decay is exponential

 

Q4. The ionising properties of radiations determine their penetration power.

A
 α-particles are not very ionising so they are easily stopped by a thin sheet of paper.
B
 α-particles are very ionising so they only travel a few centimetres in air
C
 γ-radiation can easily penetrate a sheet of card because it is very ionising
D
 γ-radiation is not very penetrating because it is very ionising

 

Q5. Protactinium has a half life of 70s. A sample of protactinium is prepared and monitored over a period of time. Which of the following statements is correct?

A
 After 140s the activity will be zero.
B
 The activity of the sample will have dropped to 25% of its initial value after 140s.
C
 The activity of the sample will have dropped to 12.5% of its initial value after 280s.
D
 The activity of the protactinium will never become zero.

 

Q6. Which of the following does not contribute to background radiation?

A
 Mobile (or cell) phones
B
 Rocks
C
 Decaying biological matter
D
 Living creatures

 

Q7. A radioactive source is placed 2.0 cm from a detector. The count rate decreases slightly if a sheet of paper is inserted between the source and the detector. It is reduced to background radiation level if the sheet of paper is replaced by a 1.0 cm thick sheet of aluminium.

Deduce what forms of radiation the source emits:

A
 Alpha radiation only
B
 Alpha and beta radiation.
C
 Beta and gamma radiation.
D
 Gamma radiation only.

The sheet of paper absorbed some of the 'count' - that due to alpha particles - the aluminium is thick enough to absorb all of the beta particles, but if there had been gamma rays they would have only been very slightly affacted by the aluminium, therefore there would have been a count higher than background remaining.

Q8. Before carrying out a radioactivity experiment it is necessary to carry out a background radiation count (so that you can calculate the background count rate). The value of that count is not affected by:

A
 The location of the experiment.
B
 The ambient temperature.
C
 The time interval used for the count.
D
 The type of detector used.

 

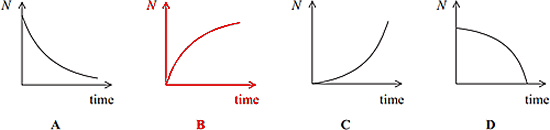
Radioactive decay is spontaneous. It is not affected by physical conditions. Therefore changes in temperature or pressure have no effect.

The location of the experiment matters because background radiation comes from furnishings, buildings and the rocks of the earth!

The longer you count - the higher the total count - the count per second (count rate) will be the same but the 'count' will change.

Not only the type of detector, but also the settings you choose on a particular detector will affect your results - never 'twiddle the knobs' on a counter mid-experiment!

 

Q9. Within a school laboratory you should always handle radioactive sources with long handled tongs and keep the time of use to a minimum. Choose from the choices below which form of radiation this safety advice most applies to, and for which reason.
Type of Radiation
Reason
A
α-particles
It is the most ionising
B
α-particles
It is the most massive
C
β-particles
It can penetrate up to a metre of air
D
β-particles
It can penetrate the skin and enter the body

 

You need to handle both sources with long handled tongs - alpha particle sources outside the body are not hazardous as they are so ionising they will be absorbed by dead skincells and not go deep enough into the body to be a problem. Beta particles can penetrate the skin, but this is less likely if the source is held as far away as possible from the skin.

Q10. Some rocks contain lead as a product of radioactive decay. Via one such decay chain a fixed quantity of polonium decays to a stable isotope of lead.

Which sketch graph best shows the number of lead atoms (N) in the sample as time progresses?

 

The lead will increase over time so it must be B or C. There will be more decays early on.... so more lead produced early on, so it must be graph B.

Q11. The sodium isotope is a radioactive isotope that can be produced by bombarding the aluminium isotope with neutrons.

Which line, A to D, in the table below correctly represents the production of from the aluminium isotopeand its subsequent decay?

 
Production
Decay
A  +     +    +  +
B  +     +    +  +
C  +     +    +  +
D  +     +    +  +

 

Charge number must be equal on both sides of the equation - therefore a helium 4 is produced - not a helium 3

That means that from the production column the answer must be A or B.

On the decay side we can see that a beta minus must be produced to balance charge - therefore the overall solution is choice B.

Q12. Artificial radioactive nuclides are manufactured by placing naturally-occurring nuclides in a nuclear reactor. They are made radioactive in the reactor as a consequence of bombardment by:

A
 gamma rays
B
 β particles.
C
 protons
D
 neutrons.

 

THIS IS CALLED ARTIFICIAL TRANSMUTATION.

Q13. A nucleus of a particular element decays, emitting a series of α and β– particles.

Which of the following series of emissions would result in an isotope of the original element?

 

A
1 α and 1 β–
B
1 α and 2 β–
C
2 α and 1 β–
D
2 α and 2 β–

 

The alpha reduces the proton number by 2 and each beta decay increases it by one.

Q14. A Geiger counter is placed near a radioactive source and different materials are placed between the source and the Geiger counter. The results of the tests are shown in the table.

Material
Count rate of Geiger counter / s–1
  
None
1000
 
Paper
1000
None absorbed - so no Alphas present
Aluminium foil
250
Quite a reduction - so betas present - but some still got though - so gamma there too
Thick steel
50
Some of the gamma absorbed

 

What is the radiation emitted by the source?

A
α only
B
α and γ
C
α and β
D
β and γ

 

Q15. Nobelium-259 has a half-life of 3500 s.

What is the decay constant of nobelium-259?

A
8.7 × 10−5 s−1
B
2.0 × 10−4 s−1
C
1.7 × 10−2 s−1
D
1.2 × 10−2 s−1

 

T½ = ln 2/λ

λ = ln 2/T½

λ = ln 2/3500

λ = 1.98 x 10-4 s-1

Choice B

Q16. A pure sample of nuclide X containing N nuclei has an activity A.

The half-life of X is 6000 years.

A pure sample of nuclide Y containing 3N nuclei has an activity 6A.

What is the half-life of nuclide Y?

A
1000 years
B
3000 years
C
12 000 years
D
18 000 years

This can be done by reasoning -

To get an activity of 6A from nuclide X you would need 6N nuclei

Y must therefore have half the half life of X for the same activity from half the number of nuclei.

Choice B

But we can do it by calculation too !

T½ = ln 2/λ and λ = A/N

So, T½ = N ln 2/A

A T½ / N = a constant

6000 A/N (for nuclide X) = 6T½/3N (for nuclide Y)

∴ T½ = 6000 A x 3N/6N = 3000

 

Q17. Cobalt-60 has a half-life of 5.27 years.

What is the total activity of 1.0 g of cobalt-60?

A
4.2 × 1013 Bq
B
2.2 × 1014 Bq
C
2.5 × 1015 Bq
D
1.3 × 1021 Bq

 

A = λN

So, we need to know the decay constant and the number of radioactive nuclei in the sample.

T½ = ln 2/λ

The activity is in Bq - that is counts per second, so we need the half life in seconds.

T½ = 5.27 years

T½ = 5.27 x 365.25 x 24 x 602 seconds

T½ = 1.66 x 108 s

λ = ln 2/T½

∴λ = ln 2/(1.66 x 108)

λ = 4.18 x 10-9 s-1

Now we need to find N - we know that there are the Avagadro mumber of nuclei in a mole of them - and that a mole has the mass of the atomic number in grammes.

So, 60g of cobalt-60 would contain 6.02 x 1023 nuclei

1g with therefore contain 6.02 x 1023/60 = 1.00 x 1022

N = 1.00 x 1022

A = λN

A = 4.18 x 10-9 x 1.00 x 1022

A = 4.18 x 1013

Choice A

Q18. When a nucleus of the radioactive isotope decays, a β- particle and an electron antineutrino are emitted.

How many protons and neutrons are there in the resulting daughter nucleus?

 
Number of protons
Number of neutrons
A
28
65
B
29
65
C
29
36
D
30
35

 

Nucleon number does not change in beta decay

Number of neutrons decreases by one and protons increase by one

Nickel - 28 protons and

65 - 28 = 37 neutrons

So product has 36 neutrons and 29 protons - choice C