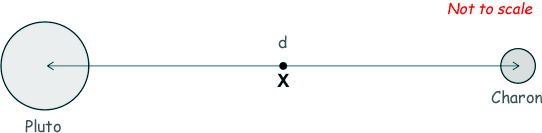Gravitational fields - Multiple Choice Q1 Masses of M and 2M exert a gravitational force F on each other when the distance between their centres is r. What is the gravitational force between masses of 2M and 4M when the distance between their centres is 4r?
Q2 A planet has a radius half the Earth's radius and a mass a quarter of the Earth's mass. What is the approximate gravitational field strength on the surface of the planet?
Q3. At the surface of the Earth the gravitational field strength is g, and the gravitational potential is V. The radius of the Earth is R. An object, whose weight on the surface of the Earth is W, is moved to a height 3R above the surface. Which line, A to D, in the table gives the weight of the object and the gravitational potential at this height?
Q4. A satellite of mass m travels in a circular orbit of radius r around a planet of mass M. Which one of the following expressions gives the angular speed of the satellite?
Q5. Which one of the following has different units to the other three?
work done = force x distance moved so J = Nm therefore J m-1 = N
Q6. The diagram shows two objects of equal mass m separated by a distance r.
Which line, A to D, in the table gives the correct values of the gravitational field strength and gravitational potential at the mid-point P between the two objects?
Gravitational field strength is a vector. Therefore pulls in opposite direction can canel each other out. At the midpoint the opposing forces will cancel the effect of each other. Therefore the result will be zero. Gravitational potential is not a vector. But work either has to be put in or is done by the system when an object is moved from a point therefore it has a sign. For an object placed at point P work would have to be done against the pull of both masses to move it to infinity - there result is therefore the sum of the potentials and the potential will be the expression not the zero
Q7. Mars has a diameter approximately 0.5 that of the Earth, and a mass of 0.1 that of the Earth.
If the gravitational potential at the Earth’s surface is –63 MJ kg–1, what is the approximate value of the gravitational potential at the surface of Mars?
Vr/M = constant so VErE/ME = VMrM/MM VM = VE x MM/ME x rE/rM VM = -63 x 0.1 x 2 = 12.6 MJ kg–1
Q8. A small mass is situated at a point on a line joining two large masses ml and m2 such that it experiences no resultant gravitational force. If its distance from the mass m1 is r1 and its distance from the mass m2 is r2, what is the value of the ratio r1/r2?
The force from each large mass on the small mass is equal in magnitude (opposite in direction) ∴ m1/r12 = m2/r22 r22/r12 = m2/m1 r12/r22 = m1/m2 r1/r2= (m1/m2)0.5
Q9. A projectile moves in a gravitational field. Which one of the following is a correct statement for the gravitational force acting on the projectile?
The projectile is a mass - the gravitational field lines show the direction that the gravitational force acts on a mass, so the answer is A. The initial movement of the projectile is at right angles to the field and its motion will follow a parabolic path... but you are not asked that!
Q10. The diagram shows two positions, X and Y, at different heights on the surface of the Earth.
Which line, A to D, in the table gives correct comparisons at X and Y for gravitational potential and angular velocity?
All points on the Earth's surface travel at the same angular velocity - the Earth rotates 360 degrees in a day and all points on it rotate through the same angle on a given time period. Gravitaional potential increases with height - GCSE stuff really!
Q11. When at the surface of the Earth, a satellite has weight W and gravitational potential energy –U. It is projected into a circular orbit whose radius is equal to twice the radius of the Earth. Which line, A to D, in the table shows correctly what happens to the weight of the satellite and to its gravitational potential energy?
Weight is due to the gravtiational pull of the planet. W = mg. Now, g = GM/r2 so Wr2 = constant W1r12 = W2r22 W1 = W r1 = r r2 = 2r ∴ Wr2 = W2 x 4r2 W2 = W/4 Gravitational potential energy is the product of mass and gravitational potential. At the surface it would be -mGM/r At height r above the surface it would be -nGM/2r - it would have halved - therefor increasing by U /2 -U + U /2 = - U /2
Q12. The graph shows how the gravitational potential, V, varies with the distance, r , from the centre of the Earth.
What does the gradient of the graph at any point represent?
V = -GM/r so Vr = a negative constant and the graph of an inverse relationship is shown in the negative quadrant. You are asked bou the gradient. The gradient of the graph is ΔV/Δr and you are given that relationship on your data sheet. ΔV/Δr = -g
Q13. Near the surface of a planet the gravitational field strength is uniform and for two points, 10 m apart vertically, the gravitational potential difference is 3 J kg–1. How much work must be done in raising a mass of 4 kg vertically through 5 m?
Points 5 metres apart will have gravitational potential difference of 1.5 J kg–1. 4 kg are lifted so 6J work is done.
Q14. What would the period of rotation of the Earth need to be if objects at the equator were to appear weightless?
The centripetal force is equal to the weight of the object if the object is just able to spin without acceleraing towards the Earth. If the weight is greater than the centripetal force it will 'fall under gravity'. If it is less than the centripetal force it will orbit out from the planet's pull. mv2/r =mg so, v2/r =g
and v = root of rg = root of (6.37 x 106 x 9.81) = =7905 Now, we can find the speed of rotation by looking at distance travelled (circumference of Earth) and time for one revolution - the period T. v = 2πr/T Equating these two calculations of speed we get: T = 2π x 6.37 x 106 /7905 = 5063 seconds = 1.4 hours Q15. The Earth has density ρ and radius R. The gravitational field strength at the surface is g. What is the gravitational field strength at the surface of a planet of density 2ρ and radius 2R?
density = mass/volume Volume depends on r3 If the radius doubles then the density will decrease by a factor of 8. In this case the planet's density has doubles - that means that the mass must have increased by a factor of 16. graviational field strength depends on mass and inversely on radius squared it therefore increases by a factor of 16 and decreases by a factor of 22 = 4. Overall that will give an increase of a factor of 16/4 = 4
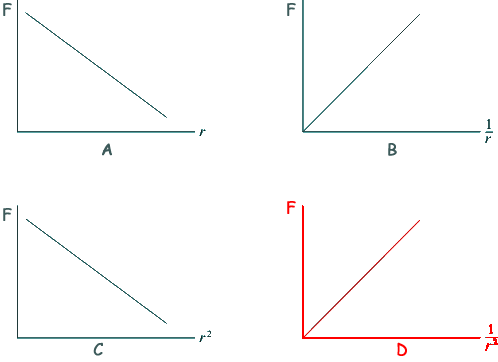
Q16. Which one of the following graphs correctly shows the relationship between the gravitational force, F, between two masses and their separation r
The relationship is an inverse squared one - so D is the solution.
Q17. Which one of the following could be a unit of gravitational potential?
Gravitational potential is 'V'. On the data sheet you have ΔW (work in joules) = VΔm (mass in kg) Q18. The radius of a certain planet is x times the radius of the Earth and its surface gravitational field strength is y times that of the Earth. Which one of the following gives the ratio
The gravitational field strength of the planet depends directly on the mass of the planet and inversely on the square of the radius. Mass = a constant x gr2 An increase of a factor of y will result from an increase of a factor of yx2 of mass. Q19. A planet of mass M and radius R rotates so rapidly that loose material at the equator only just remains on the surface. What is the period of rotation of the planet?
speed of rotation = circumference of the Earth/time period of rotation. So v = 2πR/T and T = 2πR/v When loose material only just stays in place it means that the centripetal force is equal to the weight of the object if the object is just able to spin without acceleraing towards the Earth. If the weight is greater than the centripetal force it will 'fall under gravity'. If it is less than the centripetal force it will orbit out from the planet's pull. mv2/R =mg so, v2 =gR From the equation sheet g = GM/R2 so v2 = GM/R and v = square root of (GM/R) Therefore T = 2πR / square root of (GM/R) T = 2πR x square root of (R/GM) T = 2π x square root of (R3/GM)
Q20. As a comet orbits the Sun the distance between the comet and the Sun continually changes. As the comet moves towards the Sun this distance reaches a minimum value. Which one of the following statements is incorrect as the comet approaches this minimum distance?
Q21. Which one of the following statements about Newton's law of gravitation is correct? Newton's law of gravitation explains
Q22. If an electron and proton are separated by a distance of 5 × 10–11m, what is the approximate gravitational force of attraction between them?
F = 6.67 x 10-11 x 9.11 x 10
Q23.A spherical planet of uniform density ρ has radius R. Which line, A to D, in the table gives correct expressions for the mass of the planet and the gravitational field strength at its surface?
There is no need for equation manipulation here - it is a matter of reasoning....
Q24. Charon is a moon of Pluto that has a mass equal to 1/9 that of Pluto.
The distance between the centre of Pluto and the centre of Charon is d. X is the point at which the resultant gravitational field due to Pluto and Charon is zero. What is the distance of X from the centre of Pluto?
g = GM/r2 At X: Pluto's gravitational field = Charon's gravitational field GM/X2 = GM/9(d-X)2 Cancel G and M X2 = 9(d - X)2 taking the root of each side, we get X = 3(d - X) X = 3d - 3X So 4X = 3d X = ¾d Choice C Q25. The distance between the Sun and Mars varies from 2.1 × 1011 m to 2.5 × 1011 m. When Mars is closest to the Sun, the force of gravitational attraction between them is F. What is the force of gravitational attraction between them when they are furthest apart?
F ∝1/r2 F1r12 = F2r22 F(2.1 × 1011)2 = F2(2.5 × 1011)2 F2 = F x (2.1 × 1011)2/(2.5 × 1011)2 F2 = F x 2.12/2.52 F2 = 0.71F Choice A Q26. A satellite X of mass m is in a concentric circular orbit of radius R about a planet of mass M.
What is the kinetic energy of X?
In a circular orbit: F = mv2/r So for the satellite: v = √(FR/m) The force holding it in orbit is gravitational, so: F = GMm/R2 ∴ the velocity of the satellite is given by v = √[(GmM/R2) x (R/m)] v = √(GM/R) Now, the kinetic energy of the satellite is given by EK = ½mv2, so: EK = ½m(GM/R) EK = GMm/2R Choice A
|
Follow me...
|