| Section 3.5.1- Radioactivity |
| Syllabus Detail |
You should be able to: |
Evidence for the nucleus:
Qualitative study of Rutherford Scattering |
 Explain how Rutherford's experiment made us rethink what atoms were like Explain how Rutherford's experiment made us rethink what atoms were like
 Understand the function of the prts of the equipment used. Understand the function of the prts of the equipment used.
 Know the observations made and what they made Rutherford understand about the atom. Know the observations made and what they made Rutherford understand about the atom.
Now try some  |
Radioactivity α, β and γ their properties and experimental identification; applications, e.g. to relative hazards of exposure to humans
The experimental investigation of the inverse square law for γ rays
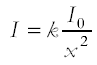
Applications, e.g. to safe handling of radioactive sources Background radiation; its origins and experimental elimination from calculations |
 recall the charge, mass, penetration power (hence how to distinguish them) and ionizing power of each type of radiation recall the charge, mass, penetration power (hence how to distinguish them) and ionizing power of each type of radiation
 recall how to perform an experiment using a radioactive source safely. recall how to perform an experiment using a radioactive source safely.
 Explain how the ISL relates to safety rule of keeping the source as far from you as possible. Explain how the ISL relates to safety rule of keeping the source as far from you as possible.
 Recall sources of background radiation and how to eliminate it from calculations and practical data. Recall sources of background radiation and how to eliminate it from calculations and practical data.
|
Random nature of decay - constant decay probability for a given nucleus

Half-life and decay constant and their determination from graphical decay data including decay curves and log graphs;
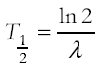
Applications, e.g. relevance to storage of waste radioactive materials; radioactive dating
|
recall that radioactive activity is:
 spontaneous (probability of a decay cannot be changed by changing pressure/temperature etc.) spontaneous (probability of a decay cannot be changed by changing pressure/temperature etc.)
 random - direction that ray is emitted or which nucleus will decay when - is impossible to say! But when dealing with large numbers of atoms the mathematics of probability can be employed. random - direction that ray is emitted or which nucleus will decay when - is impossible to say! But when dealing with large numbers of atoms the mathematics of probability can be employed.
 Recall that radioactive decay is an exponential process therefore probability is applicable! Recall that radioactive decay is an exponential process therefore probability is applicable!
You should be able to
 sketch a graph of number of nuclei against time (marking on multiples of No and T (half) to show th exponential relationship) sketch a graph of number of nuclei against time (marking on multiples of No and T (half) to show th exponential relationship)
 recall that the rate of decay recall that the rate of decay N/ N/ t (or Activity of the sample) is proportional to the number of atoms of the radioisotope present in the sample. t (or Activity of the sample) is proportional to the number of atoms of the radioisotope present in the sample.
 Recall that the decay constant ( Recall that the decay constant (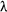 ) is the constant of proportionality between activity and sample size. It gives a measure of the probability that a particular nucleus in a sample will decay in a given time. It has units of time-1.(The negative sign before it is because the number present decreases with time - so that would lead to a negative constant!) ) is the constant of proportionality between activity and sample size. It gives a measure of the probability that a particular nucleus in a sample will decay in a given time. It has units of time-1.(The negative sign before it is because the number present decreases with time - so that would lead to a negative constant!)
 recall that the half life of a radioisotope is the time taken for half of the radioactive nuclei of that isotope substance in a sample to decay. This is constant for any given isotope. The units are those of time. recall that the half life of a radioisotope is the time taken for half of the radioactive nuclei of that isotope substance in a sample to decay. This is constant for any given isotope. The units are those of time.
 appreciate the variation in natural half-lifes from nanoseconds to millions of years and the affect this has on uses and safeguards when disposing of waste. appreciate the variation in natural half-lifes from nanoseconds to millions of years and the affect this has on uses and safeguards when disposing of waste.
 know about carbon dating. know about carbon dating.
Now try some questions - I suggest Q4, Q6, Q8 and Q9 from this link 
|
Variation of N with Z for stable and unstable nuclei Graph of N against Z for stable and unstable nuclei |
 recall that Z is the atomic number (proton number) recall that Z is the atomic number (proton number)
 sketch this graph - with labelled axes and values! sketch this graph - with labelled axes and values!
 mark in alpha, beta and positron emitters mark in alpha, beta and positron emitters
 know that positron emitters are the result of artificial transmutation experiments know that positron emitters are the result of artificial transmutation experiments
|
Possible modes of decay of unstable nuclei : alpha, beta (plus and minus), neutron and electron capture
Changes of Z and A caused by decay and representation in simple decay equations |
 modes of decay - don't forget the neutrinos! - check out the Feynman diagrams that you did in module 1 modes of decay - don't forget the neutrinos! - check out the Feynman diagrams that you did in module 1
 decay equations should be most simple for you! decay equations should be most simple for you!
Now try some questions - I suggest Q1, Q7 and Q10 from this link  |
Existence of nuclear excited states
γ ray emission
Application, e.g. use of technetium 99m as a gamma source in medical diagnosis
|
- when the nucleus emits a radioactive particle the nucleons left are not all necessarily in their lowest possible energy state - they therefore emit a gamma ray as the 'rearrange' themselves into a more stable configuration
- You should know the reasons why Tc99m is so valued and how it is used
|
|
- probing matter can be done by shooting particles into the nucleus (scattering) and making conclusions on its structure by what happens (recoil, deflection or the knocking out of another particle)
- the Rutherford experiment did this!
- as well as alpha particles high energy protons, neutrons, deuterium nuclei and electrons can be used
- (from unit 4) you should recall how charged particles repel each other and be able to interpret the way that the particles produced make traces in a magnetic field (charged ones get deflected - use FLHR to determine the charge)
|
Nuclear radius Estimation of radius from closest approach of alpha particles and determination of radius from electron diffraction; knowledge of typical values Dependence of radius on nucleon number
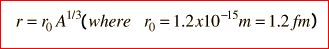
derived from experimental data
Calculation of nuclear density. |
- recall that the nucleus is measured in femtometres whereas the atom itself is of the order of angstrom units (10-10m)
- probing matter can be done by shooting particles into the nucleus (scattering) and making conclusions on its structure by what happens (recoil, deflection or the knocking out of another particle)
- See Rutherford expt. - as well as alpha particles high energy protons, neutrons, deuterium nuclei and electrons can be used to probe matter (remember particle accelerators as from unit 4?)
- be able to interpret the way that the particles produced make traces in a magnetic field (charged ones get deflected - use FLHR to determine the charge)
- understand that if an alpha particle is shot at a nucleus it will experience electrostatic repulsion and come to a stop a distance from the centre that depends on the charge in the nucleus and the kinetic energy of the particle projected at it.
- be able to evaluate the distance of closest approach as the kinetic energy of the particle would be changes into potential energy at the point of closest approach (see text book page 151 for calculation and Sang page 8)
- recall that the nucleus has a value of a few femtometres (in Rutherfords day it was thought to be of the order of 10-14m)
- understand that measurements of nuclear size can be found from electron diffraction patterns (Sang page 11-13 and text book page 152 to 153)
- know that nucleons are close-packed within the nucleus making all nuclei have the same density.
- know what to plot as graphs from the equation to find ro
- try some questions

|


