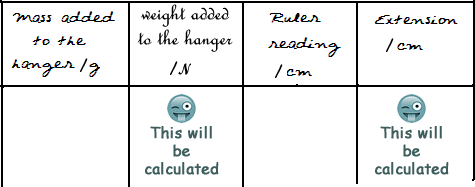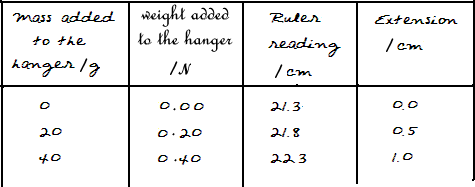Topic Menu

Hooke's Law - Stretching springs

An experiment to investigate the stretching of springs

Setting up the equipment

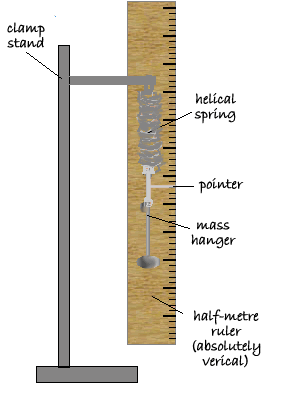The equipment was set up as shown in the diagram on the right.

A clamp stand was used to support a half metre ruler.

A helical spring was suspended from a screw jutting out of the clamp stand equipment and pointer was suspended below it.

The mass hanger was hooked under the pointer.

A blank table of results was prepared so that results could be noted down in an organised manner

Minimising Experimental Errors

The ruler was carefully viewed from all angles to ensure that it was vertical (unlike the one in the photo).

A pointer was used to help read the scale on the ruler. The scale had to be viewed at eye level to avoid parallax error.

Readings of the 'ruler reading' were noted down - no mental maths involved- extensions etc. were worked out later!

The experimenter had to be sure the spring system was stationary before a reading was taken.

At the end of each set of readings the position of the ruler was adjusted before the experiment was repeated. This was to avoid 'repeat' errors (looking for the reading value from the previous set of results!)

Experimental Procedure

An initial reading was taken when only the mass hanger was suspended from the spring.

A 20g mass was then carefully slotted onto the hanger and the reading was recorded.

This step was repeated with more 20g masses until 200g had been added to the hanger.

The whole experiment was repeated after adjusting the position of the ruler - so that the initial reading was different - avoiding an error of subconciously 'looking for' the previous reading.

Recording Results

The results were recorded in a table.

It is important to record all of the readings taken and to show clearly any calculations we do from those readings.

We therefore needed a minimum of four columns (an extra one of mass/kg might be an idea):

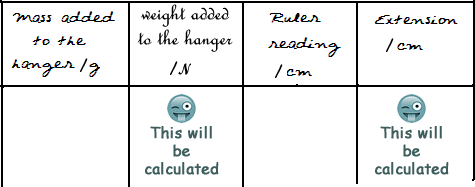
We used masses to increase the pull on the spring - we therefore needed a column to record the mass we used.

The weight of each mass added was then calculated and recorded in a separate column. Mass gets pulled by gravity. The force that that produces is called the weight. We can work out the weight exerted by the masses in our results by using the equation:

w = m g

where g = gravitational field strength of Earth = 10 N/kg

As 'g' is given in N/kg we had to change the mass in grammes into a mass in kilograms before we could calculate the weight in newtons.

The readings read from the ruler were recorded in a column and

the total extension for added weight to the hanger was calculated from these 'bare readings' on the ruler, by taking each reading away from the initial reading.

Results table (one was needed for each set of results)

Displaying results in a graph

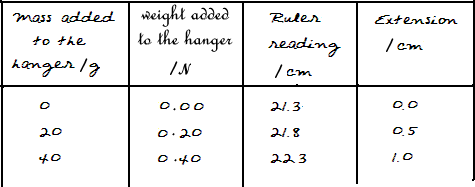
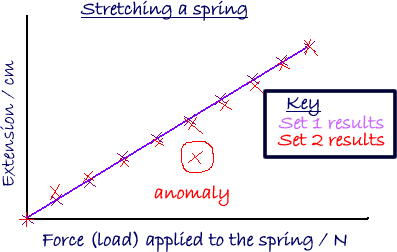
A graph was plotted of the weight added to the hanger against the extension of the spring.

The points of both sets of results were plotted on the one graph so that it was easy to identify anomalies.

This gave us a scatter graph of the results.

It showed us not only the trend of the results but also how precise our readings were.

A key explaining 'which set was which' was written on the graph.

The title of the graph indicated what the experiment involved - it did not just say what was plotted angainst what - that could be seen from the labelling of the axes!

Anomalous results were plotted, circled and repeated.

A best fit line was plotted.

These points indicated a trend of proportionality so a smooth straight line was drawn.

It did not matter whether it went through all of the points. What mattered was that it showed the general pattern that the results indicated.

Conclusion

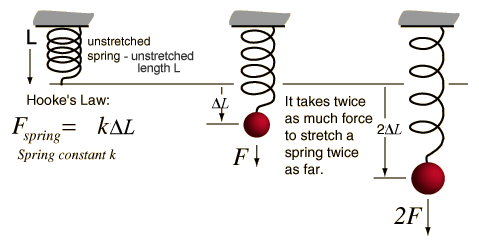
The amount the spring stretches plotted against the weight added to the hanger gives a straight line that goes through the origin. This means that the extension of a spring is directly proportional to the stretching force applied to it..

Hooke's Law states that the extension of a spring is directly proportional to the applied load (providing the elastic limit has not been exceeded)