| 3.6.1.1 Circular motion |
Motion in a circular path at constant speed implies there is an acceleration and requires a centripetal force.
Radian measure of angle.
Direction of angular velocity will not be considered.
Angular speed - ω
ω =v/r= 2πf
Centripetal acceleration - a
a = v2/r = ω2r
Centripetal force
F = mv2/r = mω2r
The derivation of a = v 2/r will not be examined. |
Remember that acceleration is rate of change of velocity - and velocity is a vector - it has direction as well as magnitude of speed associated with it.
With circular motion the object is being constantly pushed towards the circular path's centre - that is the direction of the acceleration.
 Circular Motion Multiple Choice
Questions on circular motion link to gravitational fields - motion of planets and satellites.
MS 0.4 Estimate the acceleration and centripetal force in situations that involve rotation. |
| 3.6.1.2 Simple harmonic motion (SHM) |
Analysis of the characteristic features of simple harmonic motion.
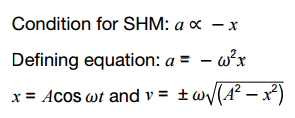
Graphical representations linking x,v,a and t
Velocity as gradient of displacement-time graph and acceleration as the gradient of the velocity-time graph..
Maximum speed = ωA
Maximum acceleration = ω2A
SHM Structured questions
|
Ensure you can define SHM - they always ask for that - 2 marks!
Get an overall appreciation of displacement from mean position, velocity and acceleration changes.
Remember that ω = 2πf
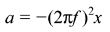
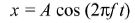
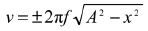
AT i, k Data loggers can be used to produce s − t, v − t and a − t graphs for SHM.
MS 3.6, 3.8, 3.9, 3.12 Sketch relationships between x, v, a and a − t for simple harmonic oscillators.
|
| 3.6.1.3 Simple harmonic systems |
Study of mass-spring system:
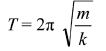
Study of simple pendulum:
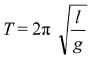
Questions may involve other harmonic oscillators (eg liquid in U-tube) but full information will be provided in questions where necessary.
Variation of Ek, Ep and total energy with displacement, and with time.
Effects of damping on oscillations. |
Practical techniques must be appreciated - this is an opportunity for the examiner to check your experimental techniques.
SHM Multiple choice
Required practical 7: Investigation into simple harmonic motion using a mass–spring system and a simple pendulum.
MS 4.6 / AT b, c Students should recognise the use of the small-angle approximation in the derivation of the time period for examples of approximate SHM. |
| 3.6.1.4 Forced vibrations and resonance |
Qualitative treatment of free and forced vibrations.
Resonance and the effects of damping on the sharpness of resonance.
Examples of these effects in mechanical systems and stationary wave situations. |
This leads to 'wordy' answers, ensure you understand all of the terms and can define them with precision.
AT g, i, k AT g, i, k Investigation of the factors that determine the resonant frequency of a driven system.
Phase difference between driver and driven displacements has been removed from the syllabus but is interesting to look at!
|
About this site
